Prediction

Overview

By the end of this practical you will know how to:

Fit regression, decision trees and random forests to training data.
Compare the fitting and prediction performance of two models for training and test data.

Tasks

A - Setup

Open your TheRBootcamp R project.
Open a new R script. At the top of the script, using comments, write your name and the date.

## NAME
## DATE
## Prediction practical

Save it as a new file called Prediction_practical.R in the 2_Code folder.
Using library() load the packages tidyverse, caret, party, partykit.

# Load packages necessary for this script
library(tidyverse)
library(caret)
library(party)
library(partykit)

Using trainControl(), create again the ctrl_none object with method = "none".

# Set training method to "none"
ctrl_none <- trainControl(method = "XX")

# Set training method to "none"
ctrl_none <- trainControl(method = "none")

Dataset 1: College graduation

B - Load the `graduation` data

Using read_csv(), read in the datasets graduation_train.csv and graduation_test.csv.

# College data
college_train <- read_csv(file = "1_Data/college_train.csv")
college_test <- read_csv(file = "1_Data/college_test.csv")

Print the data sets to make sure everything’s alright.

# Print data sets to the console
college_train

# A tibble: 500 x 18
   Private  Apps Accept Enroll Top10perc Top25perc F.Undergrad P.Undergrad
   <chr>   <dbl>  <dbl>  <dbl>     <dbl>     <dbl>       <dbl>       <dbl>
 1 Yes      1202   1054    326        18        44        1410         299
 2 No       1415    714    338        18        52        1345          44
 3 Yes      4778   2767    678        50        89        2587         120
 4 Yes      1220    974    481        28        67        1964         623
 5 Yes      1981   1541    514        18        36        1927        1084
 6 Yes      1217   1088    496        36        69        1773         884
 7 No       8579   5561   3681        25        50       17880        1673
 8 Yes       833    669    279         3        13        1224         345
 9 No      10706   7219   2397        12        37       14826        1979
10 Yes       938    864    511        29        62        1715         103
# … with 490 more rows, and 10 more variables: Outstate <dbl>,
#   Room.Board <dbl>, Books <dbl>, Personal <dbl>, PhD <dbl>, Terminal <dbl>,
#   S.F.Ratio <dbl>, perc.alumni <dbl>, Expend <dbl>, Grad.Rate <dbl>

college_test

# A tibble: 277 x 18
   Private  Apps Accept Enroll Top10perc Top25perc F.Undergrad P.Undergrad
   <chr>   <dbl>  <dbl>  <dbl>     <dbl>     <dbl>       <dbl>       <dbl>
 1 No       9251   7333   3076        14        45       13699        1213
 2 Yes      1480   1257    452         6        25        2961         572
 3 No       2336   1725   1043        10        27        5438        4058
 4 Yes      1262   1102    276        14        40         978          98
 5 Yes       959    771    351        23        48        1662         209
 6 Yes       331    331    225        15        36        1100         166
 7 Yes       804    632    281        29        72         840          68
 8 No        285    280    208        21        43        1140         473
 9 Yes       323    278    122        31        51         393           4
10 Yes       504    482    185        10        36         550          84
# … with 267 more rows, and 10 more variables: Outstate <dbl>,
#   Room.Board <dbl>, Books <dbl>, Personal <dbl>, PhD <dbl>, Terminal <dbl>,
#   S.F.Ratio <dbl>, perc.alumni <dbl>, Expend <dbl>, Grad.Rate <dbl>

Convert all character columns to factors in both training and test data using the code below.

# Convert all character features to factor
college_train <- college_train %>%
          mutate_if(is.character, factor)
college_test <- college_test %>%
          mutate_if(is.character, factor)

C - Fitting

Regression

Using train() fit a regression model called graduation_glm predicting Grad.Rateby all features. Specifically:

for the form argument, use Grad.Rate ~ ..
for the data argument, use college_train in the data argument.
for the method argument, use method = "glm" for regression.
for the trControl argument, use your ctrl_none object you created above.

# fit regression
graduation_glm <- train(form = XX ~ .,
                        data = XX,
                        method = "XX",
                        trControl = ctrl_none)

graduation_glm <- train(form = Grad.Rate ~ .,
                        data = college_train,
                        method = "glm",
                        trControl = ctrl_none)

Explore your graduation_glm object by looking at graduation_glm$finalModel and using summary(). What does the output tell you?

# show model
graduation_glm$XX
summary(XX)

graduation_glm$finalModel


Call:  NULL

Coefficients:
(Intercept)   PrivateYes         Apps       Accept       Enroll    Top10perc  
  26.320597     2.075873     0.001243    -0.000965     0.006891    -0.100378  
  Top25perc  F.Undergrad  P.Undergrad     Outstate   Room.Board        Books  
   0.289288    -0.001247    -0.001296     0.001436     0.001294    -0.000276  
   Personal          PhD     Terminal    S.F.Ratio  perc.alumni       Expend  
  -0.001756     0.060658    -0.066585     0.330961     0.195720    -0.000369  

Degrees of Freedom: 499 Total (i.e. Null);  482 Residual
Null Deviance:      189000 
Residual Deviance: 121000   AIC: 4200

summary(graduation_glm)


Call:
NULL

Deviance Residuals: 
   Min      1Q  Median      3Q     Max  
-49.27  -10.69    0.25   10.41   49.36  

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 26.320597   7.282672    3.61  0.00033 ***
PrivateYes   2.075873   2.477211    0.84  0.40245    
Apps         0.001243   0.000722    1.72  0.08554 .  
Accept      -0.000965   0.001339   -0.72  0.47151    
Enroll       0.006891   0.003663    1.88  0.06056 .  
Top10perc   -0.100378   0.110002   -0.91  0.36196    
Top25perc    0.289288   0.085752    3.37  0.00080 ***
F.Undergrad -0.001247   0.000584   -2.13  0.03328 *  
P.Undergrad -0.001296   0.000565   -2.29  0.02224 *  
Outstate     0.001436   0.000383    3.75  0.00020 ***
Room.Board   0.001294   0.000917    1.41  0.15922    
Books       -0.000276   0.005208   -0.05  0.95781    
Personal    -0.001756   0.001270   -1.38  0.16731    
PhD          0.060658   0.090671    0.67  0.50382    
Terminal    -0.066585   0.096828   -0.69  0.49200    
S.F.Ratio    0.330961   0.241530    1.37  0.17124    
perc.alumni  0.195720   0.078634    2.49  0.01315 *  
Expend      -0.000369   0.000257   -1.44  0.15098    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for gaussian family taken to be 251)

    Null deviance: 188828  on 499  degrees of freedom
Residual deviance: 121047  on 482  degrees of freedom
AIC: 4202

Number of Fisher Scoring iterations: 2

Using predict() save the fitted values of graduation_glm object as glm_fit.

# Save fitted values of regression model
glm_fit <- predict(XX)

glm_fit <- predict(graduation_glm)

Decision Trees

Using train(), fit a decision tree model called graduation_rpart predicting Grad.Rateby all features. Specifically:

for the form argument, use Grad.Rate ~ ..
for the data argument, use college_train.
for the method argument, use method = "rpart" to create decision trees.
for the trControl argument, use your ctrl_none object you created before.

# fit decision tree
graduation_rpart <- train(form = XX ~ .,
                          data = XX,
                          method = "XX",
                          trControl = XX)

# fit decision tree
graduation_rpart <- train(form = Grad.Rate ~ .,
                          data = college_train,
                          method = "rpart",
                          trControl = ctrl_none)

Explore your graduation_rpart object by looking at graduation_rpart$finalModel and plotting it with plot(as.party(graduation_rpart$finalModel)). What do you make of the output?

graduation_rpart$finalModel

n= 500 

node), split, n, deviance, yval
      * denotes terminal node

1) root 500 189000 65.4 *

plot(as.party(graduation_rpart$finalModel))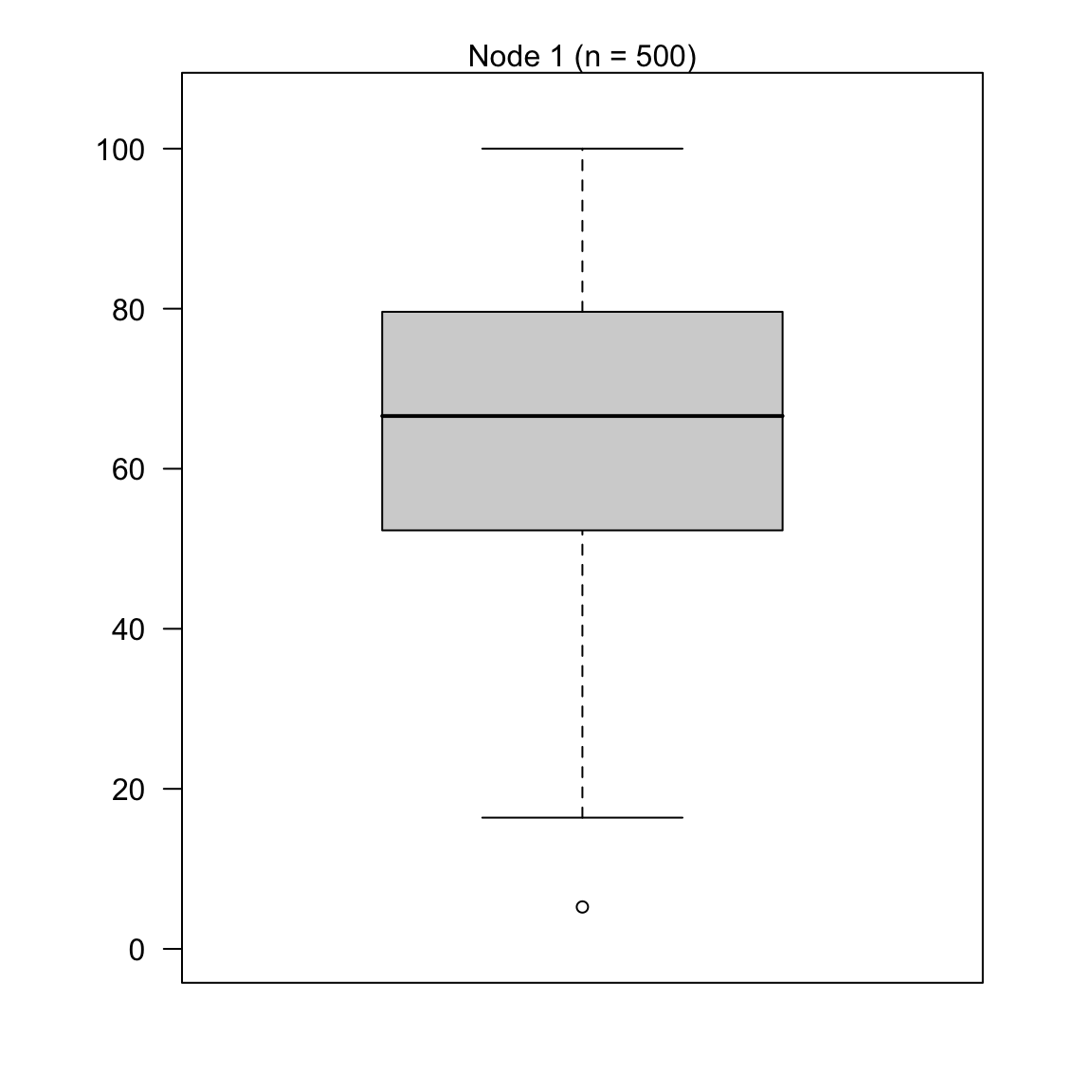

Using predict(), save the fitted values of graduation_rpart object as rpart_fit.

# Save fitted values of decision tree model
rpart_fit <- predict(XX)

rpart_fit <- predict(graduation_rpart)

Random Forests

Using train(), fit a random forest model called graduation_rf predicting Grad.Rateby all features. Specifically:

for the form argument, use Grad.Rate ~ ..
for the data argument, use college_train.
for the method argument, use method = "rf" to fit random forests.
for the trControl argument, use your ctrl_none object you created before.

# fit random forest
graduation_rf <- train(form = XX ~ .,   
                 data = XX,
                 method = "XX",
                 trControl = XX)

# fit random forest
graduation_rf <- train(form = Grad.Rate ~ ., 
                 data = college_train,
                 method = "rf",
                 trControl = ctrl_none)

Using predict(), save the fitted values of graduation_rf as rf_fit.

# Save fitted values of random forest model
rf_fit <- predict(XX)

rf_fit <- predict(graduation_rf)

Assess fitting accuracy

Save the true training criterion (Grad.Rate) in an object called criterion_train.

# Store training criterion
criterion_train <- XX$XX

# Store training criterion
criterion_train <- college_train$Grad.Rate

Using postResample(), determine the fitting performance of each of your models separately. Make sure to set your criterion_train values to the obs argument, and your true model fits XX_fit to the pred argument.

# Regression accuracy
postResample(pred = XX, obs = XX)

# Decision tree accuracy
postResample(pred = XX, obs = XX)

# Random forest accuracy
postResample(pred = XX, obs = XX)

# Regression accuracy
postResample(pred = glm_fit, obs = criterion_train)

    RMSE Rsquared      MAE 
  15.559    0.359   12.443

# Decision tree accuracy
postResample(pred = rpart_fit, obs = criterion_train)

    RMSE Rsquared      MAE 
    19.4       NA     16.0

# Random forest accuracy
postResample(pred = rf_fit, obs = criterion_train)

    RMSE Rsquared      MAE 
   6.959    0.925    5.513

What do you make of these results? Which model had the best fit?

D - Prediction

Save the criterion values from the test data set as a new object called criterion_test.

# Store test criterion
criterion_test <- XX$XX

# Store test criterion
criterion_test <- college_test$Grad.Rate

Using predict(), calculate the predicted values of each model for the test data college_test as glm_pred, rpart_pred and rf_pred.

# Regression predicted values
glm_pred <- predict(XX, newdata = XX)

# Decision trees predicted values
rpart_pred <- predict(XX, newdata = XX)

# Random forests predicted values
rf_pred <- predict(XX, newdata = XX)

# Regression predicted values
glm_pred <- predict(graduation_glm, newdata = college_test)

# Decision trees predicted values
rpart_pred <- predict(graduation_rpart, newdata = college_test)

# Random forests predicted values
rf_pred <- predict(graduation_rf, newdata = college_test)

Using postResample(), determine the prediction performance of each of your models for the test criterion criterion_test.

# Regression prediction performance
postResample(pred = XX, obs = XX)

# Decision trees prediction performance
postResample(pred = XX, obs = XX)

# Random forests prediction performance
postResample(pred = XX, obs = XX)

# Regression prediction performance
postResample(pred = glm_pred, obs = criterion_test)

    RMSE Rsquared      MAE 
  16.412    0.305   13.204

# Decision trees prediction performance
postResample(pred = rpart_pred, obs = criterion_test)

    RMSE Rsquared      MAE 
    19.6       NA     16.4

# Random forests prediction performance
postResample(pred = rf_pred, obs = criterion_test)

    RMSE Rsquared      MAE 
  15.807    0.361   12.798

How does each model’s prediction performance compare to its fitting performance? Is it worse? Better? The same? What does the change tell you about the models?

# The regression goodness of fit stayed the most constant. The random forest one droped considerably.

Which of the three models has the best prediction performance?

# The random forest predictions are still the most accurate.

If you had to use one of these three models in the real-world, which one would it be?

Dataset 2: House sales

E - Load the `house` data

Create a section in your script by copying the template below.

# House prices ------------------------------------------------------------

In this section you will analyze house sales data from King County, Washington. Run the code below to load the house_train and house_test datasets.

# house data
house_train <- read_csv(file = "1_Data/house_train.csv")
house_test <- read_csv(file = "1_Data/house_test.csv")

Print the datasets to the console to get an idea of their contents.

# Print dataframes to the console
house_train

# A tibble: 5,000 x 19
    price bedrooms bathrooms sqft_living sqft_lot floors waterfront  view
    <dbl>    <dbl>     <dbl>       <dbl>    <dbl>  <dbl>      <dbl> <dbl>
 1 176000        2      1            770     5200    1            0     0
 2 370000        2      1            850     6213    1            0     0
 3 875909        4      2.5         3610    13292    2            0     0
 4 100000        2      1            770    17334    1            0     0
 5 580000        3      1.75        1850     2797    1            0     0
 6 577000        5      2.75        1940     5000    2            0     0
 7 665000        4      2.5         2600    17388    2            0     0
 8 425000        3      1.5         1970    13709    1            0     0
 9 225000        3      1            660     6600    1            0     0
10 660000        5      2.25        2540     3750    1.5          0     0
# … with 4,990 more rows, and 11 more variables: condition <dbl>, grade <dbl>,
#   sqft_above <dbl>, sqft_basement <dbl>, yr_built <dbl>, yr_renovated <dbl>,
#   zipcode <dbl>, lat <dbl>, long <dbl>, sqft_living15 <dbl>, sqft_lot15 <dbl>

house_test

# A tibble: 1,000 x 19
    price bedrooms bathrooms sqft_living sqft_lot floors waterfront  view
    <dbl>    <dbl>     <dbl>       <dbl>    <dbl>  <dbl>      <dbl> <dbl>
 1 4.95e5        3      1.75        1890     6557      1          0     0
 2 5.90e5        3      3.5         1970     5079      2          0     0
 3 5.25e5        3      2.25        2100    40510      2          0     0
 4 3.75e5        3      1           1520    10798      1          0     0
 5 2.45e5        4      2.25        2050     7700      2          0     0
 6 1.12e6        3      2.5         4530    22873      2          0     2
 7 4.00e5        2      2.5         1340     1240      2          0     0
 8 5.33e5        4      2.75        2790     6685      2          0     0
 9 7.45e5        4      2.5         3170     5100      2          0     0
10 3.40e5        2      1            800     3090      1          0     0
# … with 990 more rows, and 11 more variables: condition <dbl>, grade <dbl>,
#   sqft_above <dbl>, sqft_basement <dbl>, yr_built <dbl>, yr_renovated <dbl>,
#   zipcode <dbl>, lat <dbl>, long <dbl>, sqft_living15 <dbl>, sqft_lot15 <dbl>

Again, a little bit of data cleaning. Convert all character features to factor.

# Convert all character to factor
house_train <- house_train %>%
          mutate_if(is.character, factor)
house_test <- house_test %>%
          mutate_if(is.character, factor)

F - Fitting

Regression

Using train(), fit a regression model called price_glm predicting the house sale price (price) using all features in house_train. Specifically:

for the form argument, use price ~ ..
for the data argument, use house_train.
for the method argument, use method = "glm" for regression.
for the trControl argument, use your ctrl_none object you created in the beginning.

# fit regression
price_glm <- train(form = price ~ .,
                   data = house_train,
                   method = "glm",
                   trControl = ctrl_none)

Explore your price_glm object by looking at price_glm$finalModel and using summary(). What do you find?

price_glm$finalModel


Call:  NULL

Coefficients:
  (Intercept)       bedrooms      bathrooms    sqft_living       sqft_lot  
     1.07e+05      -4.64e+04       5.35e+04       1.47e+02       2.31e-01  
       floors     waterfront           view      condition          grade  
     5.03e+03       6.40e+05       5.84e+04       3.03e+04       9.74e+04  
   sqft_above  sqft_basement       yr_built   yr_renovated        zipcode  
     2.40e+01             NA      -2.61e+03       4.31e+00      -5.42e+02  
          lat           long  sqft_living15     sqft_lot15  
     6.14e+05      -2.32e+05       2.71e+01      -2.63e-01  

Degrees of Freedom: 4999 Total (i.e. Null);  4982 Residual
Null Deviance:      6.81e+14 
Residual Deviance: 2.02e+14     AIC: 136000

summary(price_glm)


Call:
NULL

Deviance Residuals: 
     Min        1Q    Median        3Q       Max  
-1114590    -98269    -10834     76308   4063119  

Coefficients: (1 not defined because of singularities)
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)    1.07e+05   6.13e+06    0.02  0.98603    
bedrooms      -4.64e+04   4.14e+03  -11.19  < 2e-16 ***
bathrooms      5.35e+04   7.00e+03    7.65  2.4e-14 ***
sqft_living    1.47e+02   9.33e+00   15.73  < 2e-16 ***
sqft_lot       2.31e-01   1.02e-01    2.26  0.02360 *  
floors         5.03e+03   7.62e+03    0.66  0.50982    
waterfront     6.40e+05   3.53e+04   18.14  < 2e-16 ***
view           5.84e+04   4.52e+03   12.94  < 2e-16 ***
condition      3.03e+04   4.82e+03    6.28  3.6e-10 ***
grade          9.74e+04   4.43e+03   21.99  < 2e-16 ***
sqft_above     2.40e+01   9.25e+00    2.60  0.00935 ** 
sqft_basement        NA         NA      NA       NA    
yr_built      -2.61e+03   1.54e+02  -16.92  < 2e-16 ***
yr_renovated   4.31e+00   7.99e+00    0.54  0.58986    
zipcode       -5.42e+02   6.84e+01   -7.92  3.0e-15 ***
lat            6.14e+05   2.25e+04   27.28  < 2e-16 ***
long          -2.32e+05   2.71e+04   -8.55  < 2e-16 ***
sqft_living15  2.71e+01   7.12e+00    3.81  0.00014 ***
sqft_lot15    -2.63e-01   1.60e-01   -1.64  0.10008    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for gaussian family taken to be 4.06e+10)

    Null deviance: 6.8104e+14  on 4999  degrees of freedom
Residual deviance: 2.0203e+14  on 4982  degrees of freedom
AIC: 136339

Number of Fisher Scoring iterations: 2

Using predict(), save the fitted values of price_glm object as glm_fit.

# Store fitted values
glm_fit <- predict(price_glm)

Decision tree

Using train(), fit a decision tree model called price_rpart predicting price using all features in house_train. Specifically:

for the form argument, use price ~ ..
for the data argument, use house_train.
for the method argument, use method = "rpart" to create decision trees.
for the trControl argument, use your ctrl_none object you created before.

# fit decision tree
price_rpart <- train(form = price ~ .,
                     data = house_train,
                     method = "rpart",
                     trControl = ctrl_none)

Explore your price_rpart object by looking at price_rpart$finalModel and plotting it with plot(as.party(price_rpart$finalModel)). What do you find?

price_rpart$finalModel

n= 5000 

node), split, n, deviance, yval
      * denotes terminal node

1) root 5000 6.81e+14 537000 *

plot(as.party(price_rpart$finalModel))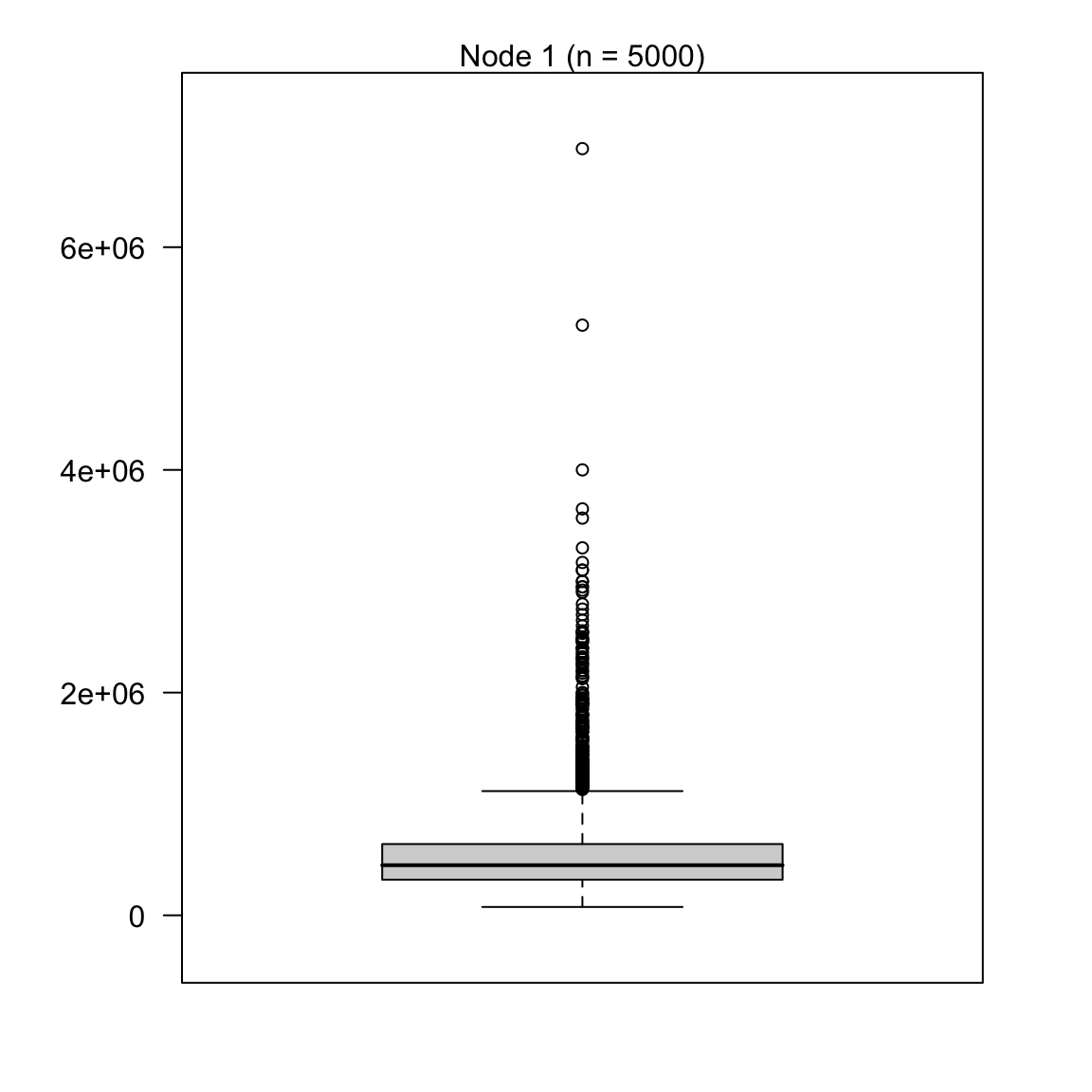

Using predict() save the fitted values of price_rpart object as rpart_fit.

# Store fitted values
rpart_fit <- predict(price_rpart)

Random Forests

Using train(), fit a random forest model called price_rf predicting price using all features in house_train. Specifically:

for the form argument, use price ~ ..
for the data argument, use house_train in the data argument.
for the method argument, use method = "rf" to fit random forests.
for the trControl argument, use your ctrl_none object you created before.

price_rf <- train(form = price ~ .,
                 data = house_train,
                 method = "rf",
                 trControl = ctrl_none)

Using predict() save the fitted values of price_rf object as rf_fit.

# store fitted values
rf_fit <- predict(price_rf)

Assess accuracy

Save the true training criterion values as a vector called criterion_train.

# store criterion
criterion_train <- house_train$price

Using postResample(), determine the fitting performance of each of your models separately.

# Regression
postResample(pred = glm_fit, obs = criterion_train)

    RMSE Rsquared      MAE 
2.01e+05 7.03e-01 1.25e+05

# Decision Trees
postResample(pred = rpart_fit, obs = criterion_train)

    RMSE Rsquared      MAE 
  369063       NA   232500

# Random Forests
postResample(pred = rf_fit, obs = criterion_train)

    RMSE Rsquared      MAE 
6.59e+04 9.75e-01 3.40e+04

Which model had the best fit? Same model as for the graduation data?

G - Prediction

Save the criterion values from the test data set as a new vector called criterion_test.

# store criterion of test data
criterion_test <- house_test$price

Using predict(), save the predicted values of each model for the test data as glm_pred, rpart_pred and rf_pred.

# Regression
glm_pred <- predict(price_glm, 
                    newdata = house_test)

# Decision Trees
rpart_pred <- predict(price_rpart, 
                      newdata = house_test)

# Random Forests
rf_pred <- predict(price_rf, 
                   newdata = house_test)

Using postResample(), determine the prediction performance of each of your models.

# Regression
postResample(pred = glm_pred, obs = criterion_test)

    RMSE Rsquared      MAE 
1.92e+05 7.03e-01 1.26e+05

# Decision Trees
postResample(pred = rpart_pred, obs = criterion_test)

    RMSE Rsquared      MAE 
  351741       NA   224747

# Random Forests
postResample(pred = rf_pred, obs = criterion_test)

    RMSE Rsquared      MAE 
1.27e+05 8.77e-01 7.49e+04

How does each model’s prediction performance compare to its fitting performance? Is it worse? Better? The same? What does the change tell you about the models?
Which of the three models has the best prediction performance?
Contemplate, if you had to use one of these three models in the real-world, which one would it be? Any different

X - Challenges:

For either dataset try to find feature sets that lead to the best possible prediction performance.

Examples

# Fitting and evaluating regression, decision trees, and random forests

# Step 0: Load packages-----------
library(tidyverse)    # Load tidyverse for dplyr and tidyr
library(caret)        # For ML mastery 
library(partykit)     # For decision trees
library(party)        # For decision trees

# Step 1: Load and Clean, and Explore Training data ----------------------

# training data
data_train <- read_csv("1_Data/mpg_train.csv")

# test data
data_test <- read_csv("1_Data/mpg_test.csv")

# Convert all characters to factor
#  Some ML models require factors
data_train <- data_train %>%
  mutate_if(is.character, factor)

data_test <- data_test %>%
  mutate_if(is.character, factor)

# Explore training data
data_train        # Print the dataset
View(data_train)  # Open in a new spreadsheet-like window 
dim(data_train)   # Print dimensions
names(data_train) # Print the names

# Define criterion_train
#   We'll use this later to evaluate model accuracy
criterion_train <- data_train$hwy

# Step 2: Define training control parameters -------------

# In this case, I will set method = "none" to fit to 
#  the entire dataset without any fancy methods
ctrl_none <- trainControl(method = "none") 

# Step 3: Train model: -----------------------------
#   Criterion: hwy
#   Features: year, cyl, displ

# Regression --------------------------
hwy_glm <- train(form = hwy ~ year + cyl + displ,
                 data = data_train,
                 method = "glm",
                 trControl = ctrl_none)

# Look at summary information
hwy_glm$finalModel
summary(hwy_glm)

# Save fitted values
glm_fit <- predict(hwy_glm)

#  Calculate fitting accuracies
postResample(pred = glm_fit, 
             obs = criterion_train)

# Decision Trees ----------------
hwy_rpart <- train(form = hwy ~ year + cyl + displ,
                data = data_train,
                method = "rpart",
                trControl = ctrl_none)

# Look at summary information
hwy_rpart$finalModel
plot(as.party(hwy_rpart$finalModel))   # Visualise your trees

# Save fitted values
rpart_fit <- predict(hwy_rpart)

# Calculate fitting accuracies
postResample(pred = rpart_fit, obs = criterion_train)

# Random Forests -------------------------
hwy_rf <- train(form = hwy ~ year + cyl + displ,
                data = data_train,
                method = "rf",
                trControl = ctrl_none)   

# Look at summary information
hwy_rf$finalModel

# Save fitted values
rf_fit <- predict(hwy_rf)

# Calculate fitting accuracies
postResample(pred = rf_fit, obs = criterion_train)

# Visualise Accuracy -------------------------

# Tidy competition results
accuracy <- tibble(criterion_train = criterion_train,
                   Regression = glm_fit,
                   DecisionTrees = rpart_fit,
                   RandomForest = rf_fit) %>%
               gather(model, prediction, -criterion_train) %>%
               # Add error measures
               mutate(se = prediction - criterion_train,
                      ae = abs(prediction - criterion_train))

# Calculate summaries
accuracy_agg <- accuracy %>%
                  group_by(model) %>%
                  summarise(mae = mean(ae))   # Calculate MAE (mean absolute error)

# Plot A) Scatterplot of truth versus predictions
ggplot(data = accuracy,
       aes(x = criterion_train, y = prediction, col = model)) +
  geom_point(alpha = .5) +
  geom_abline(slope = 1, intercept = 0) +
  labs(title = "Predicting mpg$hwy",
       subtitle = "Black line indicates perfect performance")

# Plot B) Violin plot of absolute errors
ggplot(data = accuracy, 
       aes(x = model, y = ae, fill = model)) + 
  geom_violin() + 
  geom_jitter(width = .05, alpha = .2) +
  labs(title = "Fitting Absolute Errors",
       subtitle = "Numbers indicate means",
       x = "Model",
       y = "Absolute Error") +
  guides(fill = FALSE) +
  annotate(geom = "label", 
           x = accuracy_agg$model, 
           y = accuracy_agg$mae, 
           label = round(accuracy_agg$mae, 2))

# Step 5: Access prediction ------------------------------

# Define criterion_train
criterion_test <- data_test$hwy

# Save predicted values
glm_pred <- predict(hwy_glm, newdata = data_test)
rpart_pred <- predict(hwy_rpart, newdata = data_test)
rf_pred <- predict(hwy_rf, newdata = data_test)

#  Calculate fitting accuracies
postResample(pred = glm_pred, obs = criterion_test)
postResample(pred = rpart_pred, obs = criterion_test)
postResample(pred = rf_pred, obs = criterion_test)

# Visualise Accuracy -------------------------

# Tidy competition results
accuracy <- tibble(criterion_test = criterion_test,
                   Regression = glm_pred,
                   DecisionTrees = rpart_pred,
                   RandomForest = rf_pred) %>%
               gather(model, prediction, -criterion_test) %>%
               # Add error measures
               mutate(se = prediction - criterion_test,
                      ae = abs(prediction - criterion_test))

# Calculate summaries
accuracy_agg <- accuracy %>%
                  group_by(model) %>%
                  summarise(mae = mean(ae))   # Calculate MAE (mean absolute error)

# Plot A) Scatterplot of truth versus predictions
ggplot(data = accuracy,
       aes(x = criterion_test, y = prediction, col = model)) +
  geom_point(alpha = .5) +
  geom_abline(slope = 1, intercept = 0) +
  labs(title = "Predicting mpg$hwy",
       subtitle = "Black line indicates perfect performance")

# Plot B) Violin plot of absolute errors
ggplot(data = accuracy, 
       aes(x = model, y = ae, fill = model)) + 
  geom_violin() + 
  geom_jitter(width = .05, alpha = .2) +
  labs(title = "Prediction Absolute Errors",
       subtitle = "Numbers indicate means",
       x = "Model",
       y = "Absolute Error") +
  guides(fill = FALSE) +
  annotate(geom = "label", 
           x = accuracy_agg$model, 
           y = accuracy_agg$mae, 
           label = round(accuracy_agg$mae, 2))

Datasets

File	Rows	Columns
college_train.csv	500	18
college_test.csv	277	18
house_train.csv	5000	21
house_test.csv	1000	21

The college_train and college_test data are taken from the College dataset in the ISLR package. They contain statistics for a large number of US Colleges from the 1995 issue of US News and World Report.
The house_train and house_test data come from https://www.kaggle.com/harlfoxem/housesalesprediction

Variable description of `college_train` and `college_test`

Name	Description
`Private`	A factor with levels No and Yes indicating private or public university.
`Apps`	Number of applications received.
`Accept`	Number of applications accepted.
`Enroll`	Number of new students enrolled.
`Top10perc`	Pct. new students from top 10% of H.S. class.
`Top25perc`	Pct. new students from top 25% of H.S. class.
`F.Undergrad`	Number of fulltime undergraduates.
`P.Undergrad`	Number of parttime undergraduates.
`Outstate`	Out-of-state tuition.
`Room.Board`	Room and board costs.
`Books`	Estimated book costs.
`Personal`	Estimated personal spending.
`PhD`	Pct. of faculty with Ph.D.’s.
`Terminal`	Pct. of faculty with terminal degree.
`S.F.Ratio`	Student/faculty ratio.
`perc.alumni`	Pct. alumni who donate.
`Expend`	Instructional expenditure per student.
`Grad.Rate`	Graduation rate.

Variable description of `house_train` and `house_test`

Name	Description
`price`	Price of the house in $.
`bedrooms`	Number of bedrooms.
`bathrooms`	Number of bathrooms.
`sqft_living`	Square footage of the home.
`sqft_lot`	Square footage of the lot.
`floors`	Total floors (levels) in house.
`waterfront`	House which has a view to a waterfront.
`view`	Has been viewed.
`condition`	How good the condition is (Overall).
`grade`	Overall grade given to the housing unit, based on King County grading system.
`sqft_above`	Square footage of house apart from basement.
`sqft_basement`	Square footage of the basement.
`yr_built`	Built Year.
`yr_renovated`	Year when house was renovated.
`zipcode`	Zip code.
`lat`	Latitude coordinate.
`long`	Longitude coordinate.
`sqft_living15`	Living room area in 2015 (implies some renovations). This might or might not have affected the lotsize area.
`sqft_lot15`	lot-size area in 2015 (implies some renovations).

Functions

Packages

Package	Installation
`tidyverse`	`install.packages("tidyverse")`
`caret`	`install.packages("caret")`
`partykit`	`install.packages("partykit")`
`party`	`install.packages("party")`

Functions

Function	Package	Description
`trainControl()`	`caret`	Define modelling control parameters
`train()`	`caret`	Train a model
`predict(object, newdata)`	`stats`	Predict the criterion values of `newdata` based on `object`
`postResample()`	`caret`	Calculate aggregate model performance in regression tasks
`confusionMatrix()`	`caret`	Calculate aggregate model performance in classification tasks

Resources

Cheatsheet

Prediction

Machine Learning with R The R Bootcamp

Overview

Tasks

A - Setup

B - Load the graduation data

C - Fitting

Regression

Decision Trees

Random Forests

Assess fitting accuracy

D - Prediction

E - Load the house data

F - Fitting

Regression

Decision tree

Random Forests

Assess accuracy

G - Prediction

X - Challenges:

Examples

Datasets

Variable description of college_train and college_test

Variable description of house_train and house_test

Functions

Packages

Functions

Resources

Cheatsheet

Machine Learning with R
The R Bootcamp

B - Load the `graduation` data

E - Load the `house` data

Variable description of `college_train` and `college_test`

Variable description of `house_train` and `house_test`