Unsupervised learning

Überblick

In diesem Practical wirst die Clusteranalyse an zwei Datensätzen üben.

Am Ende des Practicals wirst du wissen wie man:

Cluster anhand verschiedener Methoden identifiziert.
Wie man die Anzahl der Cluster in den Daten schätzt.

Aufgaben

A - Setup

Öffne dein TheRBootcamp R project. Es sollte die Ordner 1_Data und 2_Code enthalten. Stelle sicher, dass du alle Datensätze, welche im Datensätze Tab aufgelisted sind, in deinem 1_Data Ordner hast.
Öffne ein neues R Skript. Schreibe deinen Namen, das Datum und “Unsupervised learning Practical” als Kommentare an den Anfang des Skripts.

## NAME
## DATUM
## Unsupervised learning Practical

Speichere das neue Skript unter dem Namen unspervised_learning_practical.R im 2_Code Ordner.
Lade die Pakete tidyverse, cstab, dbscan, und mclust.

B - Lade den `gap` Datensatz

Verwende die read_csv() Funktion um den Datensatz gap.csv als Objekt gap einzulesen.

# Lese gap.csv
gap <- read_csv('1_Data/gap.csv')

Printe den Datensatz.
Verwende summary() um einen weiteren Überblick über die Daten zu bekommen.
Verwende den Code unten um einen neuen Datensatz mit ausschliesslich den Daten aus dem Jahr 2007 und den beiden Variablen Lebenserwartung und BIP pro Kopf zu erstellen.

# gap in 2007
gap2007 <- gap %>% 
  filter(Jahr == 2007) %>% 
  select(`BIP pro Kopf`, Lebenserwartung)

C - k-means

Verwende die kmeans() Funktion um den gap2007 Datensatz in 3 Cluster aufzuteilen.

# kmeans für gap in 2007
gap2007_km <- kmeans(x = XX, centers = XX)

# kmeans für gap in 2007
gap2007_km <- kmeans(x = gap2007, centers = 3)

Printe gap2007_km in die Console und studiere den Output.

# kmeans für gap in 2007
gap2007_km

K-means clustering with 3 clusters of sizes 27, 80, 34

Cluster means:
  BIP pro Kopf Lebenserwartung
1        34099            79.9
2         2809            60.3
3        13701            72.1

Clustering vector:
  [1] 2 2 2 2 3 1 1 1 2 1 2 2 2 3 3 3 2 2 2 2 1 2 2 3 2 2 2 2 2 3 2 3 3 3 1
 [36] 2 2 2 2 2 3 2 2 1 1 3 2 1 2 1 2 2 2 2 2 1 3 1 2 2 3 2 1 1 1 2 1 2 2 2
 [71] 3 3 2 2 3 2 2 3 2 2 3 3 2 3 2 2 2 2 2 1 1 2 2 2 1 3 2 3 2 2 2 3 3 3 2
[106] 3 2 2 3 2 3 2 1 3 1 2 3 1 2 2 2 1 1 2 1 2 2 2 3 2 3 2 1 1 3 3 2 2 2 2
[141] 2

Within cluster sum of squares by cluster:
[1] 9.86e+08 3.76e+08 6.82e+08
 (between_SS / total_SS =  90.7 %)

Available components:

[1] "cluster"      "centers"      "totss"        "withinss"    
[5] "tot.withinss" "betweenss"    "size"         "iter"        
[9] "ifault"

Die erste Zeile und die Tabelle Cluster means geben Aufschluss darüber, welche Cluster das Modell identifiziert hat.
Ganz unten im Output steht eine Liste der im Objekt enthaltenen Elemente. Verwende gap2007_km$XX um das Element cluster als eigenes Objekt clusters und das Element centers als eigenes Objekt centers zu speichern.

# gap2007_km 
clusters <- gap2007_km$cluster
centers <- gap2007_km$centers

Verwende den Code unten um eine Abbildung mit den Daten mit Clusterzuweisungen zu erstellen. Wenn ihr damit vertraut seit, dürft ihr dafür natürlich auch ggplot2 benutzen.

# kmeans plot für gap in 2007
plot(gap2007, col = clusters)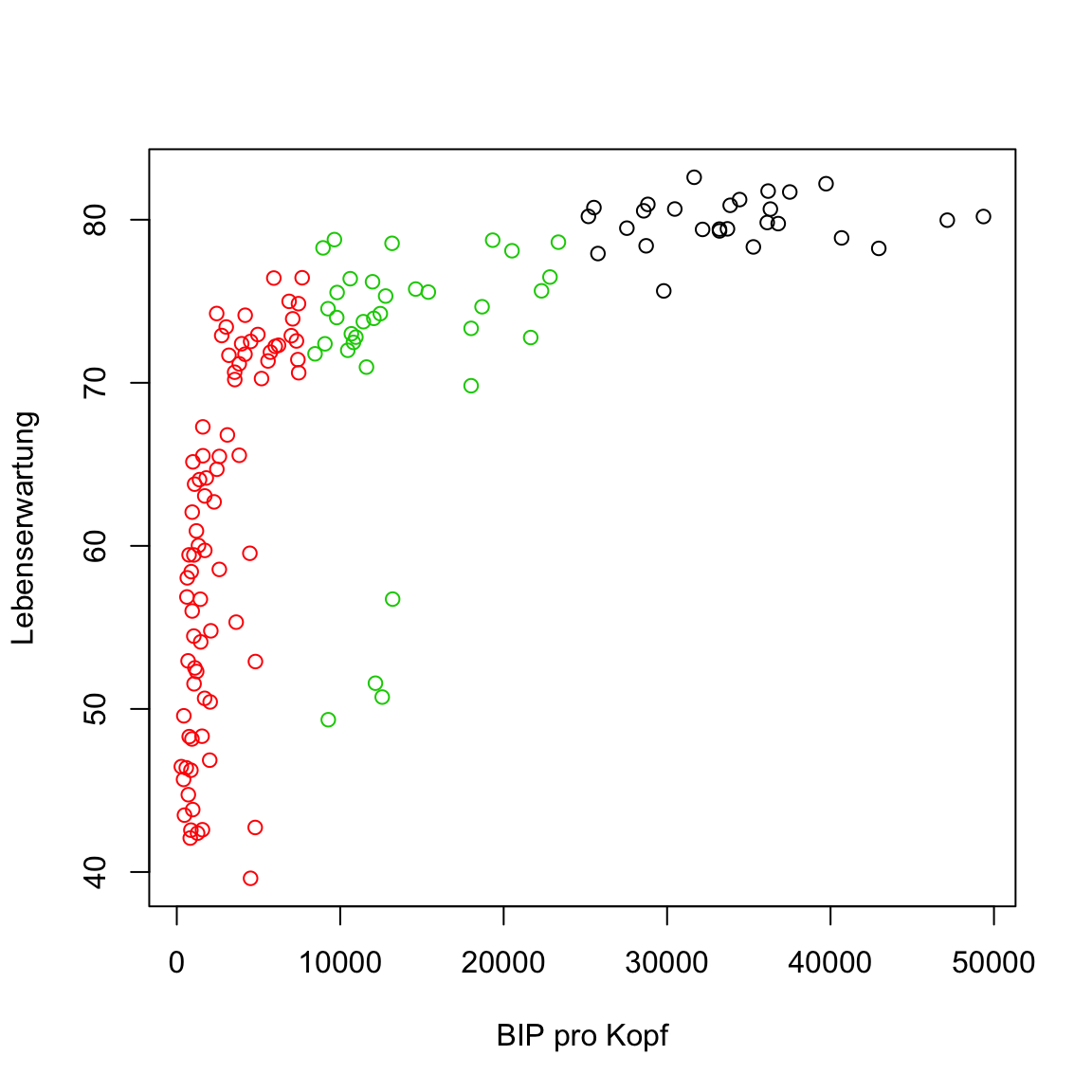

Mit dem Code unten ergänze nun die Zentroide der Cluster.

# kmeans plot für gap in 2007
plot(gap2007, col = clusters)
points(centers, pch = 16, col = 1:3, cex = 2)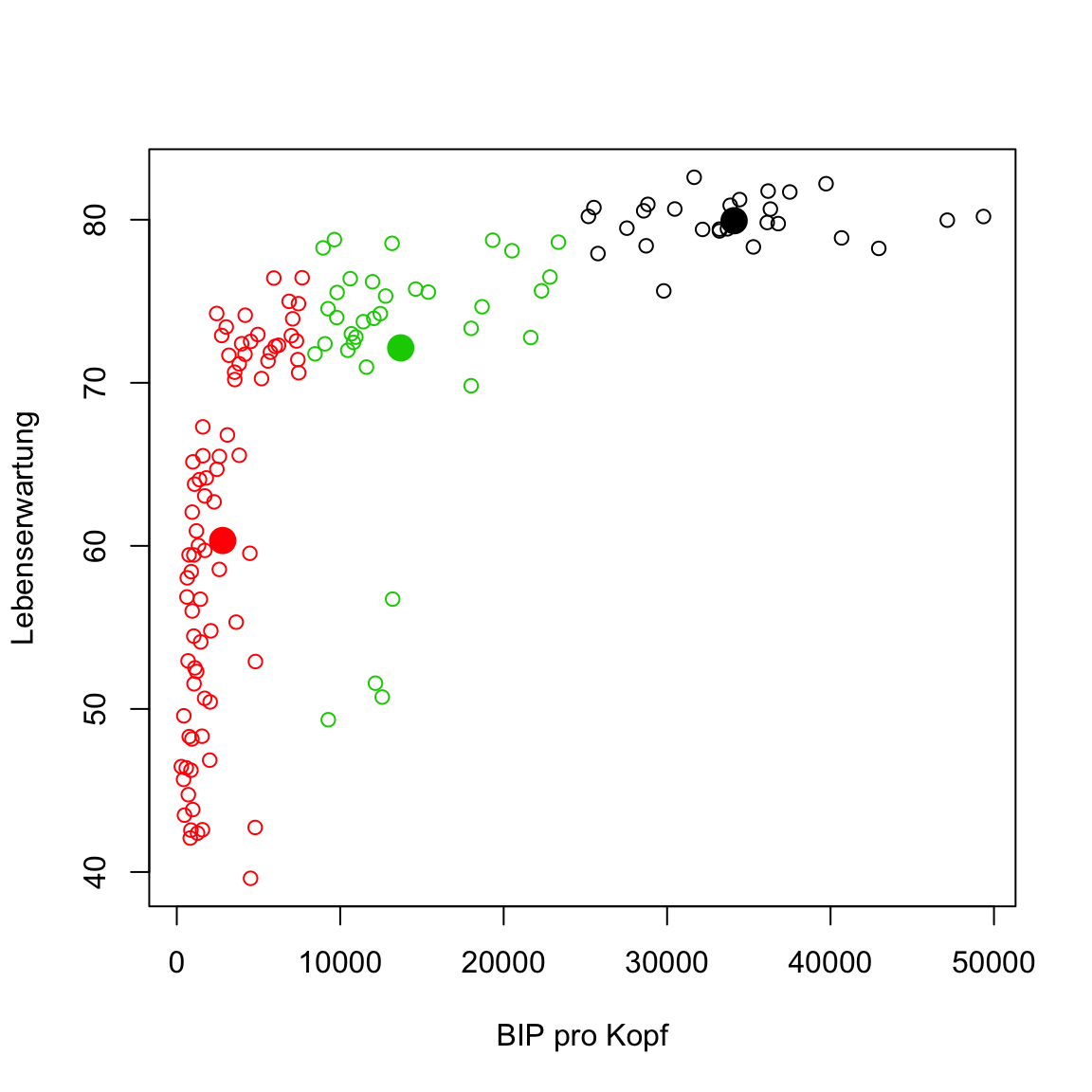

Etwas ist seltsam oder? Einige der Punkte des mittleren Clusters scheinen eigentlich deutlich näher am unteren als am eigenen Cluster zu liegen. Das sollte nicht sein. Hast du eine Idee wie das zustande kommen konnte?
Das Problem ist, dass die Variablen sehr verschiedene Skalen haben. Die Werte von BIP pro Kopf sind deutlich grösser und damit absolut gesehen weiter voneinander entfernt: Der Unterschied zwischen 10000 und 20000 BIP pro Kopf ist deutlich grösser als der zwischen 50 und 60 Jahren Lebenserwartung. Aus diesem Grund spielt BIP pro Kopf bei der Zuweisung zu den Clustern eine deutlich grössere Rolle als Lebenserwartung. Um dieses Problem zu beheben verwende den Code unten um einen neuen Datensatz mit standardisierten Featuren zu generieren.

# standardisiere gap in 2007
gap2007_stand <- gap2007 %>% 
  scale %>% 
  as_tibble()

Nun führe nochmals kmeans() aus, diesmal mit gap2007_stand und plotte die Daten mit den neuen Clusterzuweisungen. Problem behoben?

# kmeans plot für gap in 2007 (standardisiert)
gap2007_stand_km <- kmeans(x = gap2007_stand, centers = 3) 

# extrahiere Elemente
clusters <- gap2007_stand_km$cluster
centers <- gap2007_stand_km$centers

# plot
plot(gap2007_stand, col = clusters)
points(centers, pch = 16, col = 1:3, cex = 2)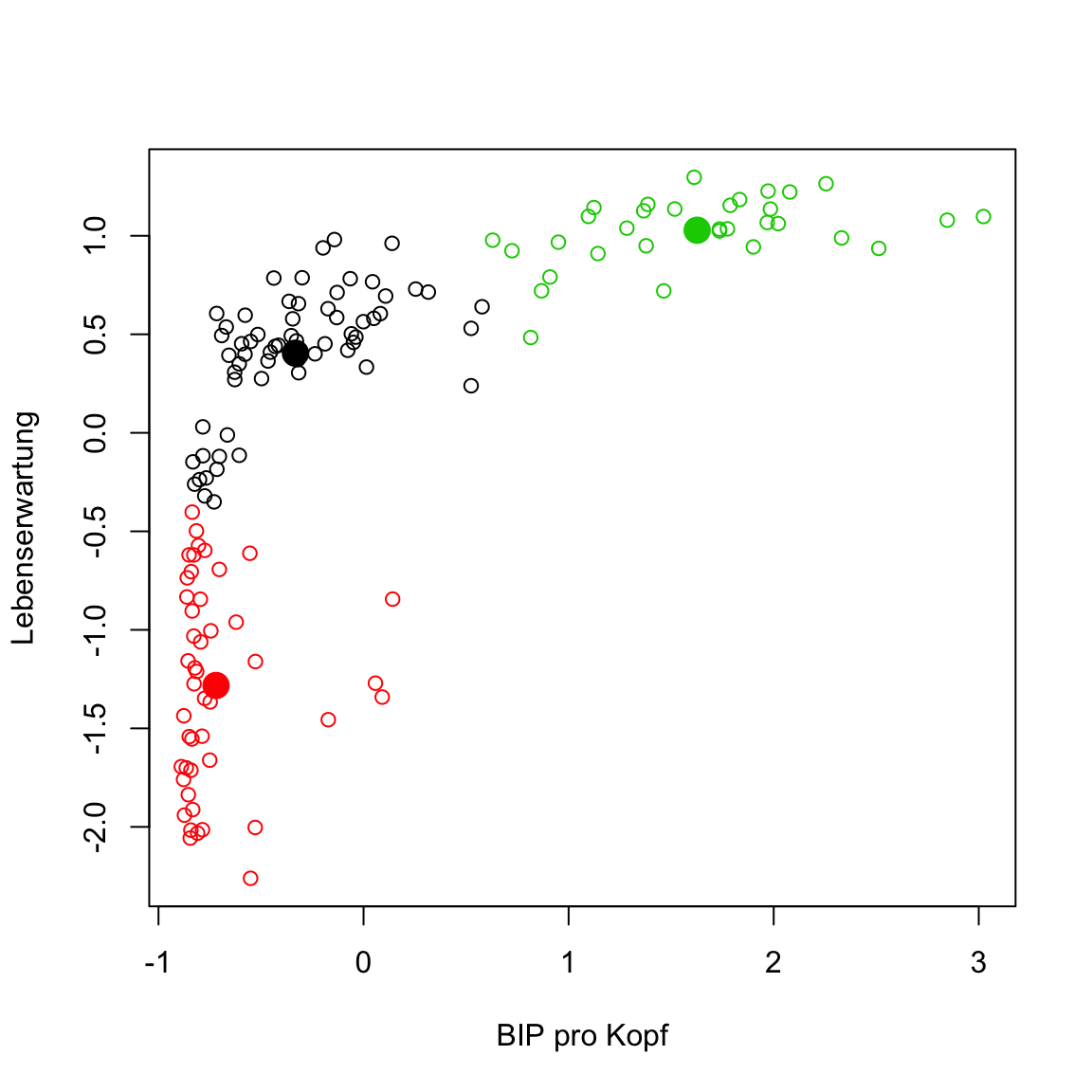

D - k-selection

Nun verwende den Code unten um einen Verlauf der Binnenvarianz für kmeans zu erstellen für potentielle Clusteranzahlen 2:20. Der Code verwendet die map() Funktion des Pakets purrr. Das Paket wird dabei mit purrr:: explizit angesprochen, weil es ansonsten ggf. zu Verwechslungen mit der map Funktion des mclust Pakets käme. Benutze die standardisierten Daten gap2007_stand.

# binnenvarianz über kmeans verlauf
km_verlauf <- purrr::map(2:20, kmeans, x = gap2007_stand)
binnenvarianz <- purrr::map_dbl(km_verlauf, 
                               `[[`, i = 'tot.withinss')

Benutze plot(XX) um den Verlauf der binnenvarianz zu plotten.

# kmeans plot für gap in 2007 (standardisiert)
plot(binnenvarianz)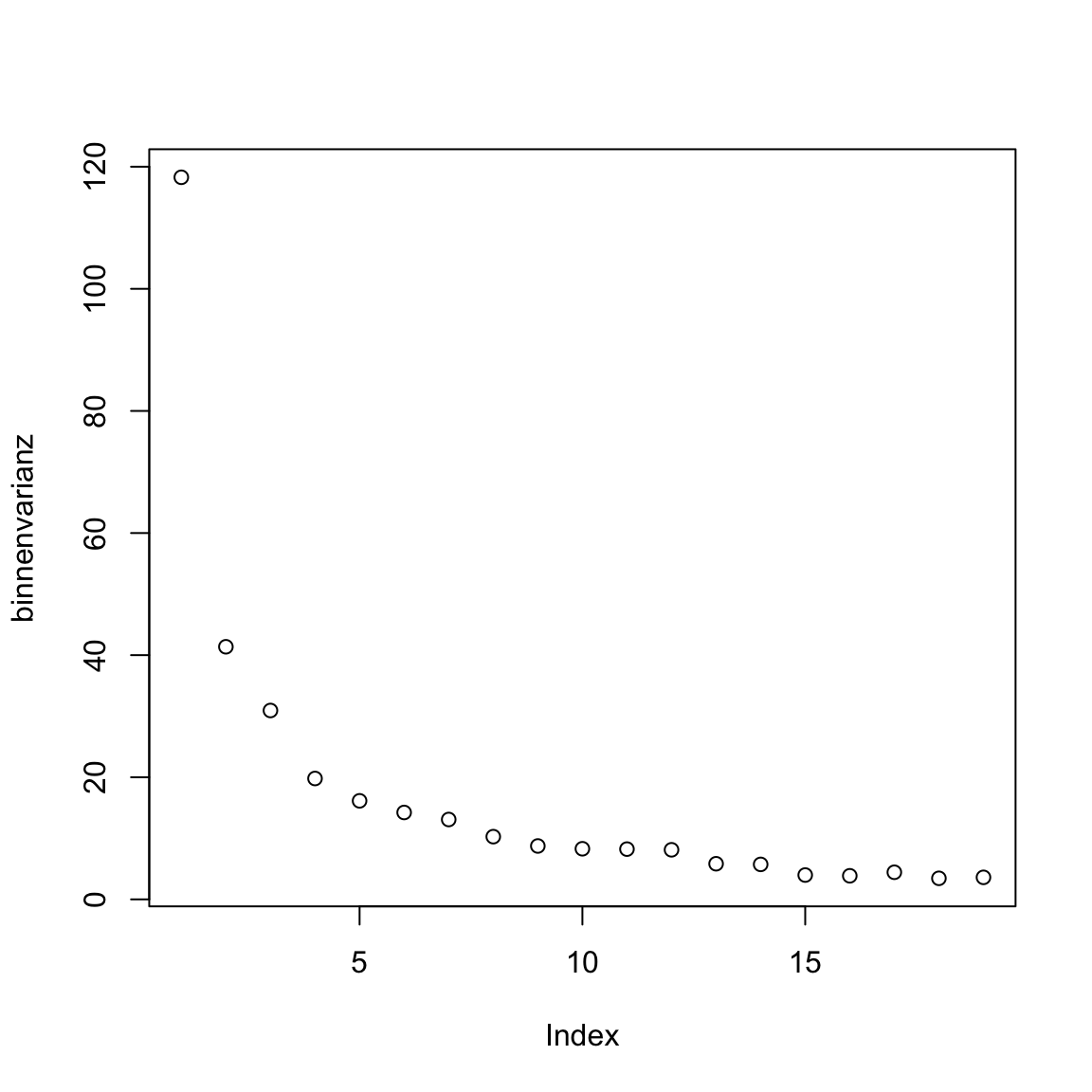

Was sagt euch der Plot? Gibt es Ellbogen im Verlauf, die bestimmte Werte für k nahelegen?
Auf Basis des Verlaufs erscheinen verschiedene Werte für k plausibel: 1, 3, oder 7. Verwende die cDistance() Funktion aus dem cstab Paket im Code unten um Schätzungen für k innerhalb der Werte 2:20 auf Basis der Gap- und Slope-Statistik zu erhalten.

# schätze k mit cstab
k_est <- cDistance(data = as.matrix(XX),
                   kseq = XX:XX)

# schätze k mit cstab
k_est <- cDistance(data = as.matrix(gap2007_stand),
                   kseq = 2:20)

Lass dir mit k_est$k_Gap und k_est$k_Slope ausgeben. Sinnvolle Schätzungen?

# schätze k mit cstab
k_est$k_Gap

[1] 14

k_est$k_Slope

[1] 3

Versuche nun das selbe mit cStability(). Lass dir im Anschluss den Wert k_instab ausgeben. Sinnvoller?

# schätze k mit cstab
k_est <- cStability(data = as.matrix(gap2007_stand),
                   kseq = 2:20)



========
===============
======================
==============================
======================================
=============================================
====================================================
============================================================
====================================================================
===========================================================================

k_est$k_instab

[1] 3

Notiz: Erinnere dich, es gibt kein richtiges k. Aus diesem Grund ist in Fällen, in denen die Clusterlösung visuell inspiziert werden kann, das Augenmass der etablierte Goldstandard. Bei mehr als zwei Features wird dies natürlich zunehmend schwieriger, sodass einem nichts anderes übrig bleibt als sich auf komputationale Verfahren zu stützen.

E - DBSCAN

Verwende dbscan() aus dem dbscan Paket um die Daten erneut zu clustern. Hier ist es erneut essentiell, die standardisierten Daten gap2007_stand zu verwenden, da ansonsten der eps Parameter effektiv keinen Kreis, sondern eine sehr, sehr flache Ellipse beschreibt. Nur wenn alle Features die selbe Skala haben, bedeutet eps eine Distanz der gleichen Grösse für alle Feature. Setze eps auf .5.

# clustere mit DBSCAN
gap2007_stand_dbscan <- dbscan(x = XX, 
                               eps = XX)

# clustere mit DBSCAN
gap2007_stand_dbscan <- dbscan(x = gap2007_stand, 
                               eps = .5)

Printe das Objekt gap2007_stand_dbscan um es zu inspizieren.
Was verrät euch der Output? Erinnert euch ein Cluster von 0 bedeutet Outlier.
Ein einzelner Cluster und 5 Outlier wurden identifiziert. Schaut euch das Ergenis an indem ihr wie oben das Element cluster extrahiert und dann die Daten mit eingefärbten Clustern plottet. Das + 1 ist notwendig, weil ein Wert von 0 keine Farbe bedeutet.

# extrahiere Elemente
clusters <- gap2007_stand_dbscan$XX

# plot
plot(XX, col = XX + 1)

# extrahiere Elemente
clusters <- gap2007_stand_dbscan$cluster

# plot
plot(gap2007_stand, col = clusters + 1)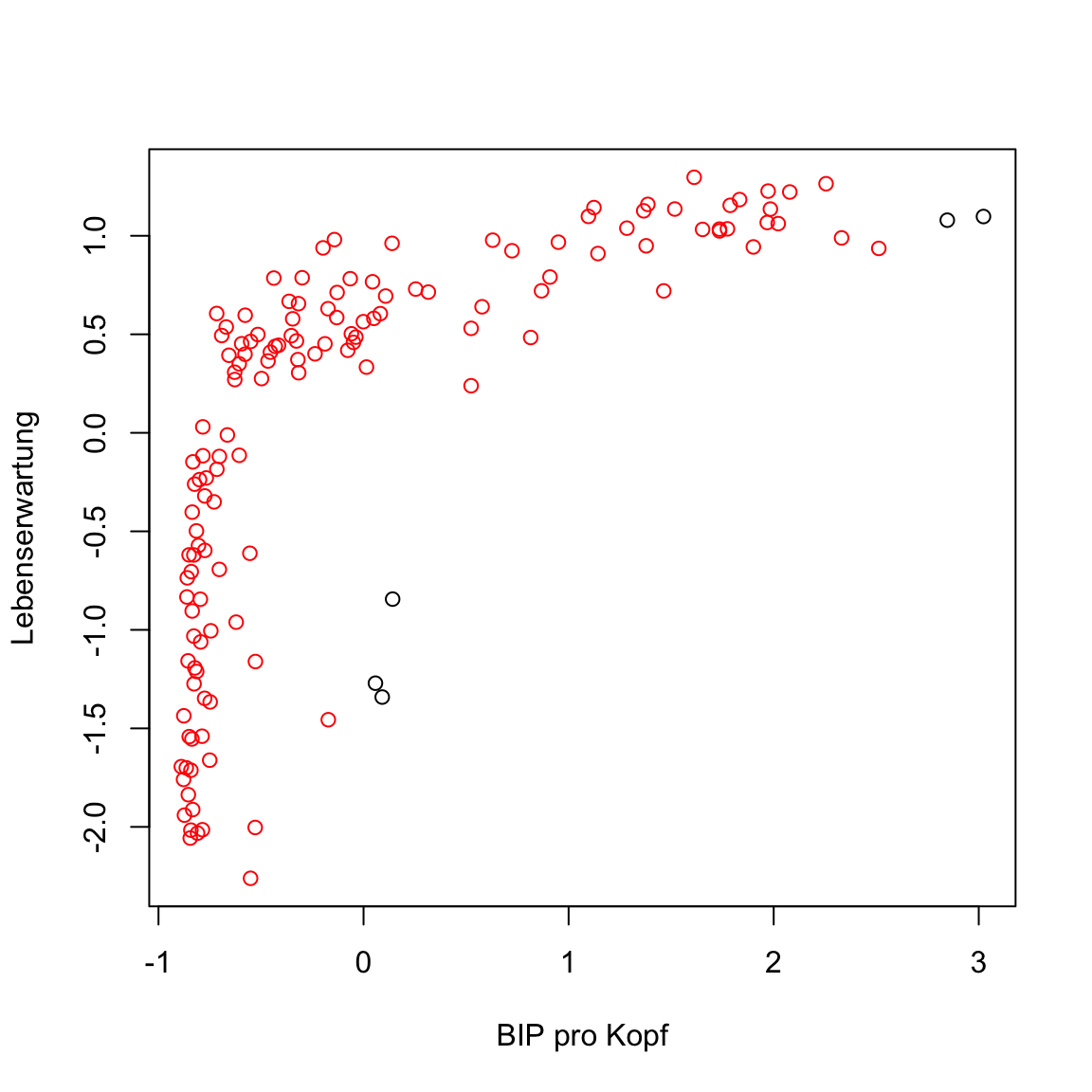

Lasse dbscan() erneut laufen, aber mit anderen Werten für eps. Versuche eps = .3 und eps = .1 und plotte jeweils das Ergebnis. Ändert sich was?

# clustere mit DBSCAN
gap2007_stand_dbscan.3 <- dbscan(x = gap2007_stand, eps = .3)
gap2007_stand_dbscan.1 <- dbscan(x = gap2007_stand, eps = .1)

# plot
par(mfrow = c(1, 3))
plot(gap2007_stand, col = gap2007_stand_dbscan$cluster + 1)
plot(gap2007_stand, col = gap2007_stand_dbscan.3$cluster + 1)
plot(gap2007_stand, col = gap2007_stand_dbscan.1$cluster + 1)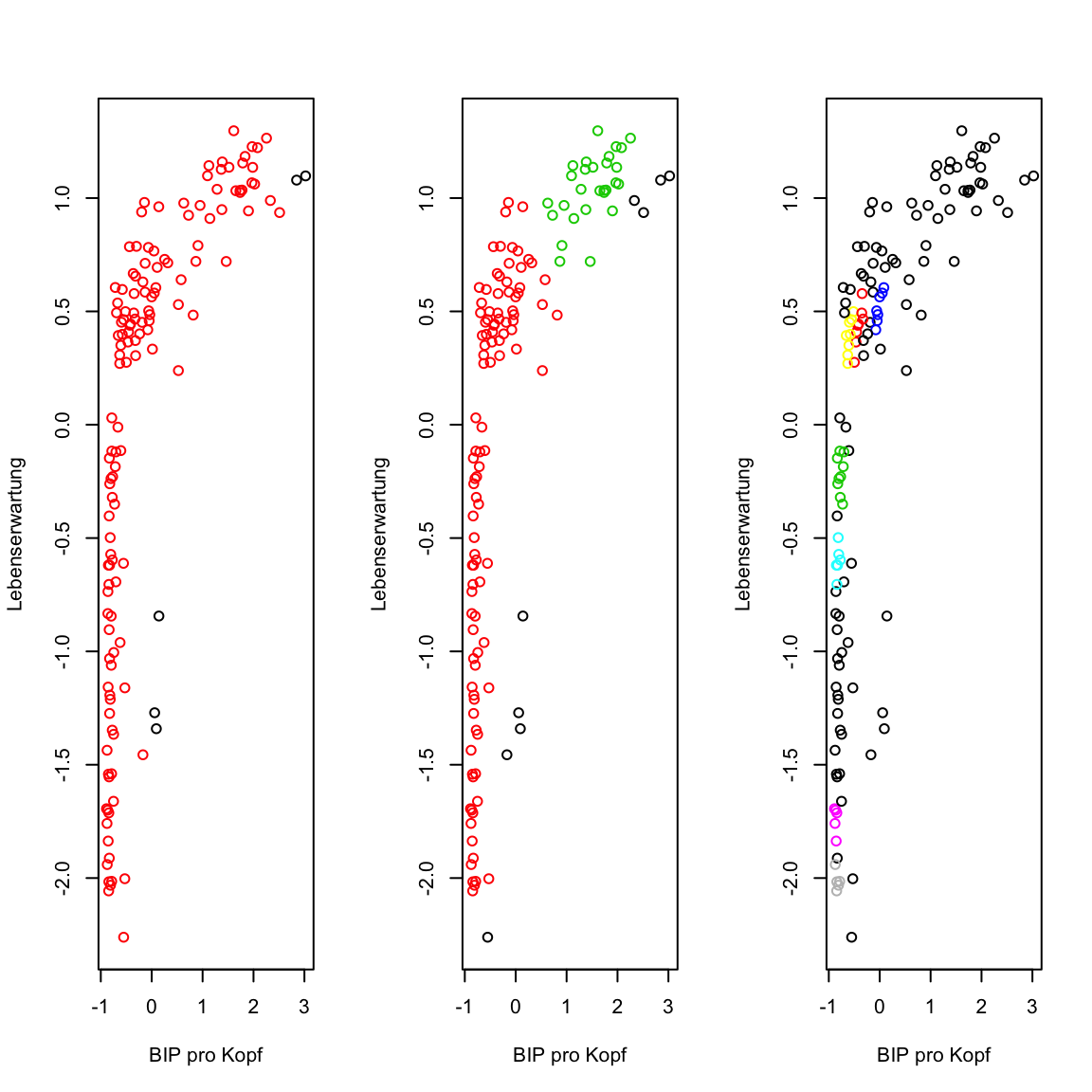

dbscan hat einen weiteren Parameter minPts, welcher bestimmt, wie viele Punkte in einem Abstand von eps liegen müssen, damit der Punkt ein Kernpunkt wird. Versuche ein paar verschiedene Werte und versuche zu verstehen was passiert.

F - Gaussian Mixtures

Zum Abschluss, verwende Mclust() aus dem mclust Paket um über Gaussian Mixture Modelle die Cluster zu bestimmen. Arbeite hier mit dem nicht-standardisierten Datensatz gap2007. Dies ist möglich, weil Gaussian Mixtures die Skalen der Variablen automatisch berücksichtigt.

# clustere mit Gaussian mixtures
gap2007_gm <- Mclust(XX)

# clustere mit Gaussian mixtures
gap2007_gm <- Mclust(gap2007)

Printe das Objekt gap2007_gm um es zu inspizieren.
Der Output verrät relativ wenig, nur welche Elemente enthalten sind. Verwende table(gap2007_gm$classification) um einen Überblick über die Clusterzuweisungen zu erhalten. Wie viele Cluster wurden identifiziert?
Verwende das classification Element um wie üblich die Daten mit den Clusterzuweisungen zu plotten.

# plot
plot(gap2007_stand, col = gap2007_gm$classification)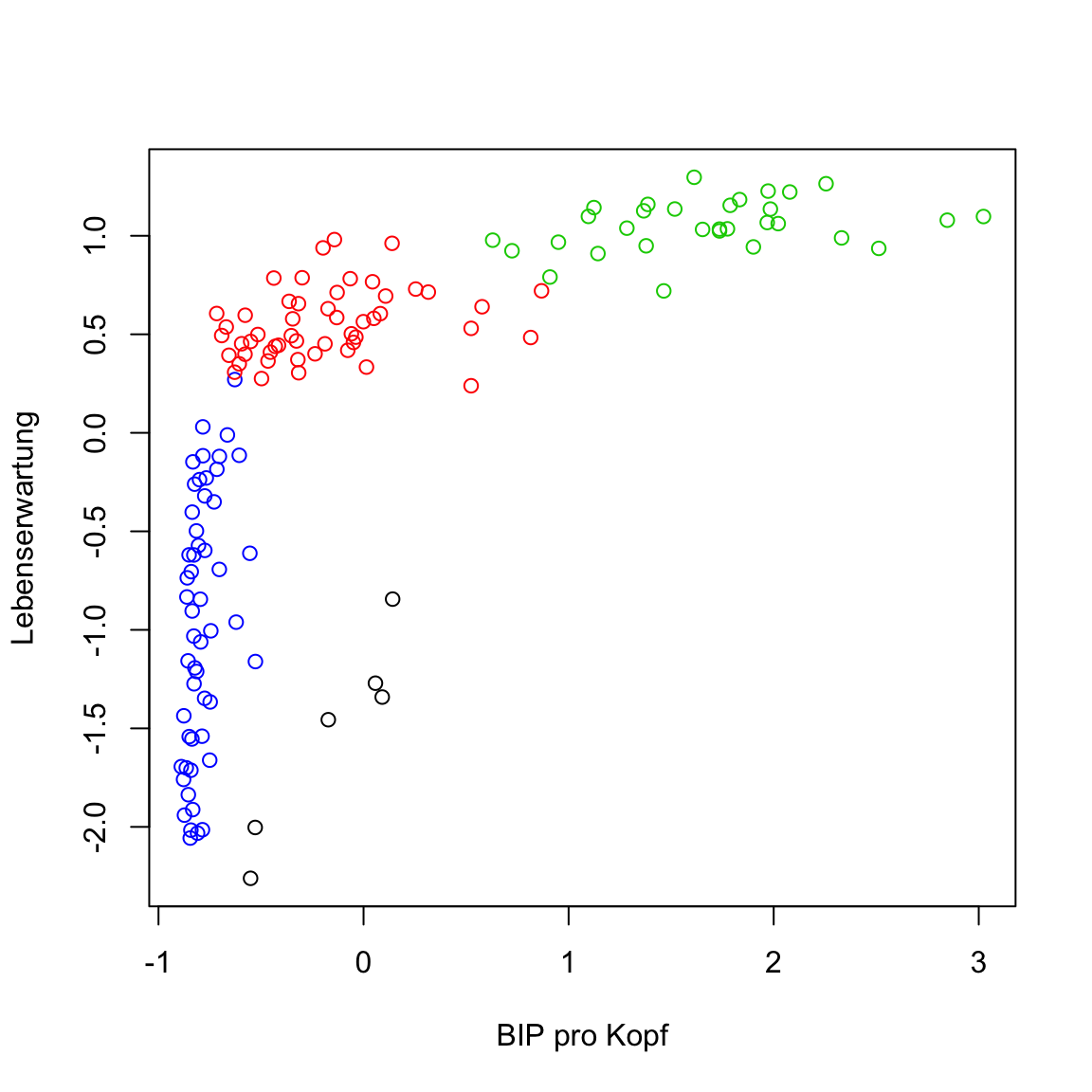

Führe nun alternativ plot(gap2007_gm, what = 'classification') aus, um den eigenen Plot des mclust Pakets zu sehen.

# plot
plot(gap2007_gm, what = 'classification')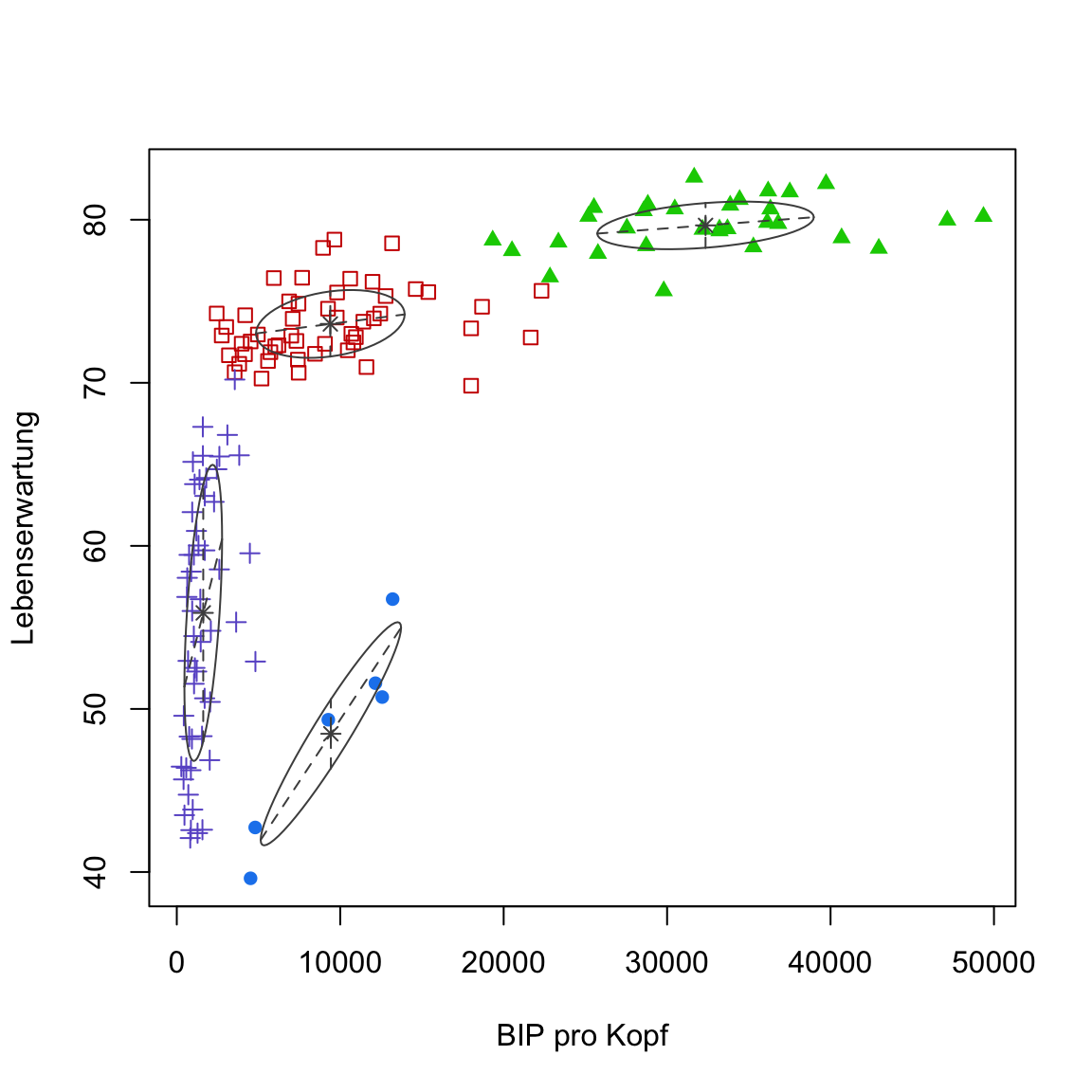

Versuche nachzuvollziehen was der mclust Plot euch zeigt. Erinnere dich, die Ellipsen sind Normalverteilungen, die jeweils eigene Skalen und Feature-Zusammenhänge berücksichtigen können.
Eine interessante Eigenschaft von Gaussian Mixtures ist, dass man direkt die Unsicherheit der Clusterzuweisung evaluieren kann. Führe plot(gap2007_gm, what = 'uncertainty') aus. Die Grössen der Punkte zeigen an, wie gross die Unsicherheit (oder Rivalität) in der Zuweisung der Punkte zu den Clustern war.

# plot
plot(gap2007_gm, what = 'uncertainty')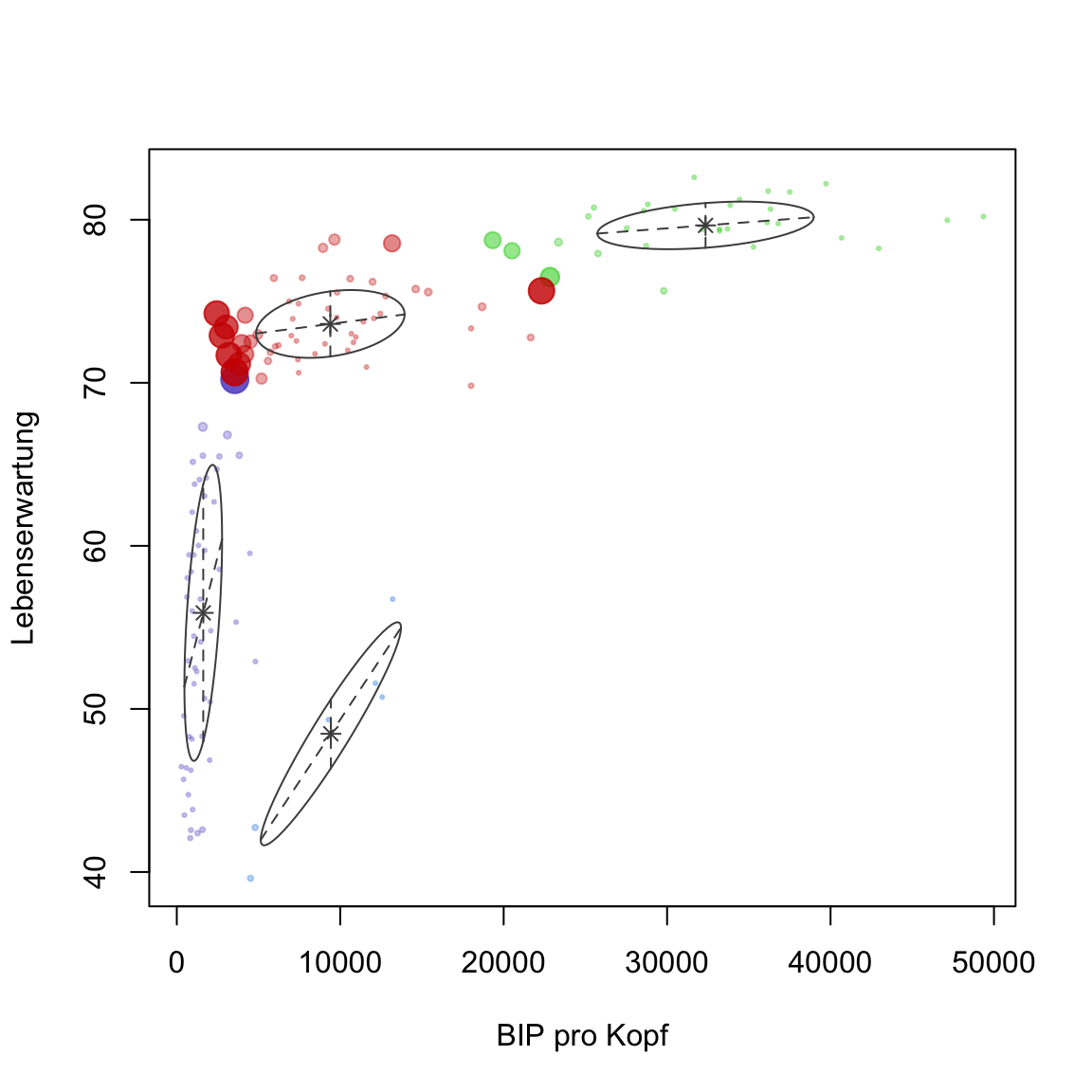

X - Challenges: Modellselektion Gaussian mixtures

Eine nützliche Eigenschaft der Mclust() Funktion ist, dass parallel verschieden komplexe Varianten des Modells mit verschiedenem k geschätzt werden und dass am Ende nicht nur das beste k ausgewählt wird, sondern die beste Kombination von k und Modell. Du erhälst einen Überblick über den Prozess mit plot(gap2007_gm, what = 'BIC').

# plot
plot(gap2007_gm, what = 'BIC')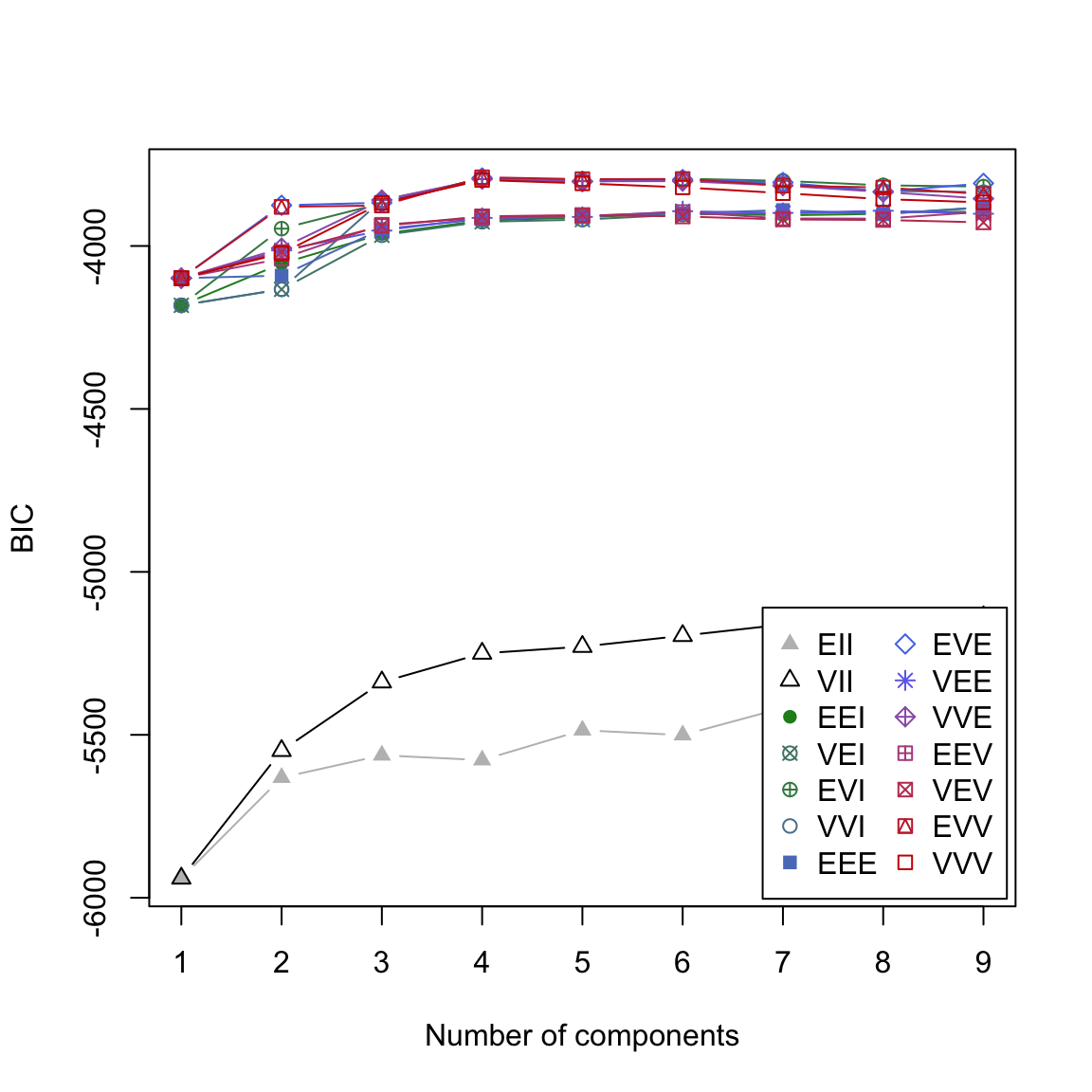

BIC ist das sogenannte Bayesian Information Criterion und dient der Auswahl eines Modells unter Berücksichtigung der Komplexität des Modells. In diesem Fall sind hohe Werte besser. In der Abbildung siehst du nun wie sich der BIC Wert über verschiedene k (Number of components) und Modelle (verschiedene Linien) entwickelt.

Verwende plot(gap2007_gm, what = 'BIC', ylim = c(-4200, -3900)) um einen besseren Ausschnitt zu erhalten. Nun solltest du sehen können, dass das EVV Modell den besten BIC für 4 Komponenten erzielt. Entsprechend wurde dieses Modell ausgewählt.

# plot
plot(gap2007_gm, what = 'BIC', ylim = c(-4200, -3900))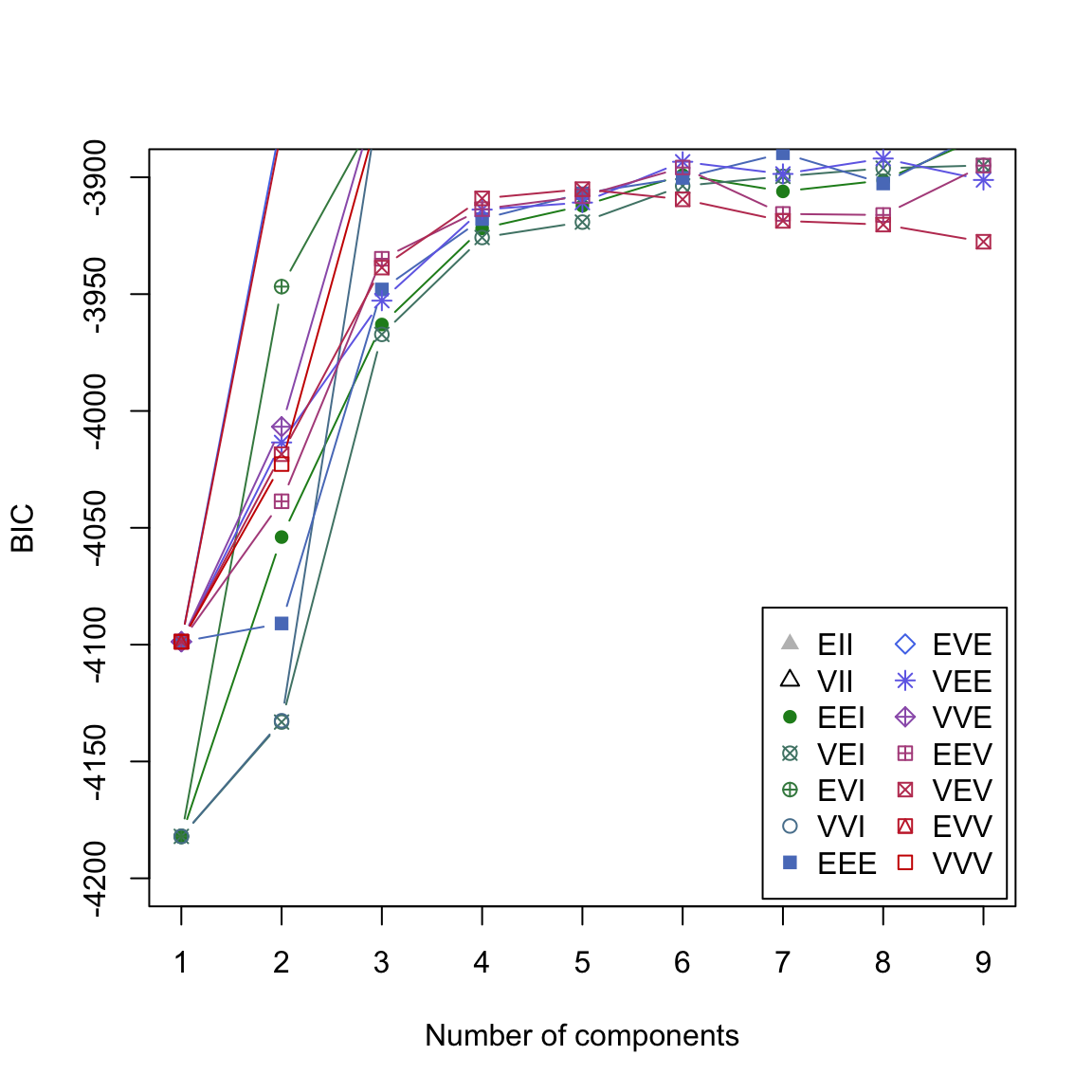

Lasse dir mit ?mclustModelNames die Erläuterung zu den Modellbezeichnungen anzeigen. Dort findest zu heraus, dass das Modell annimmt, dass das Volumen der einzelnen Cluster (hier die Fläche der Ellipsoide) gleich ist. Dies lässt sich auch in plot(gap2007_gm, what = 'classification') erkennen.

plot(gap2007_gm, what = 'classification')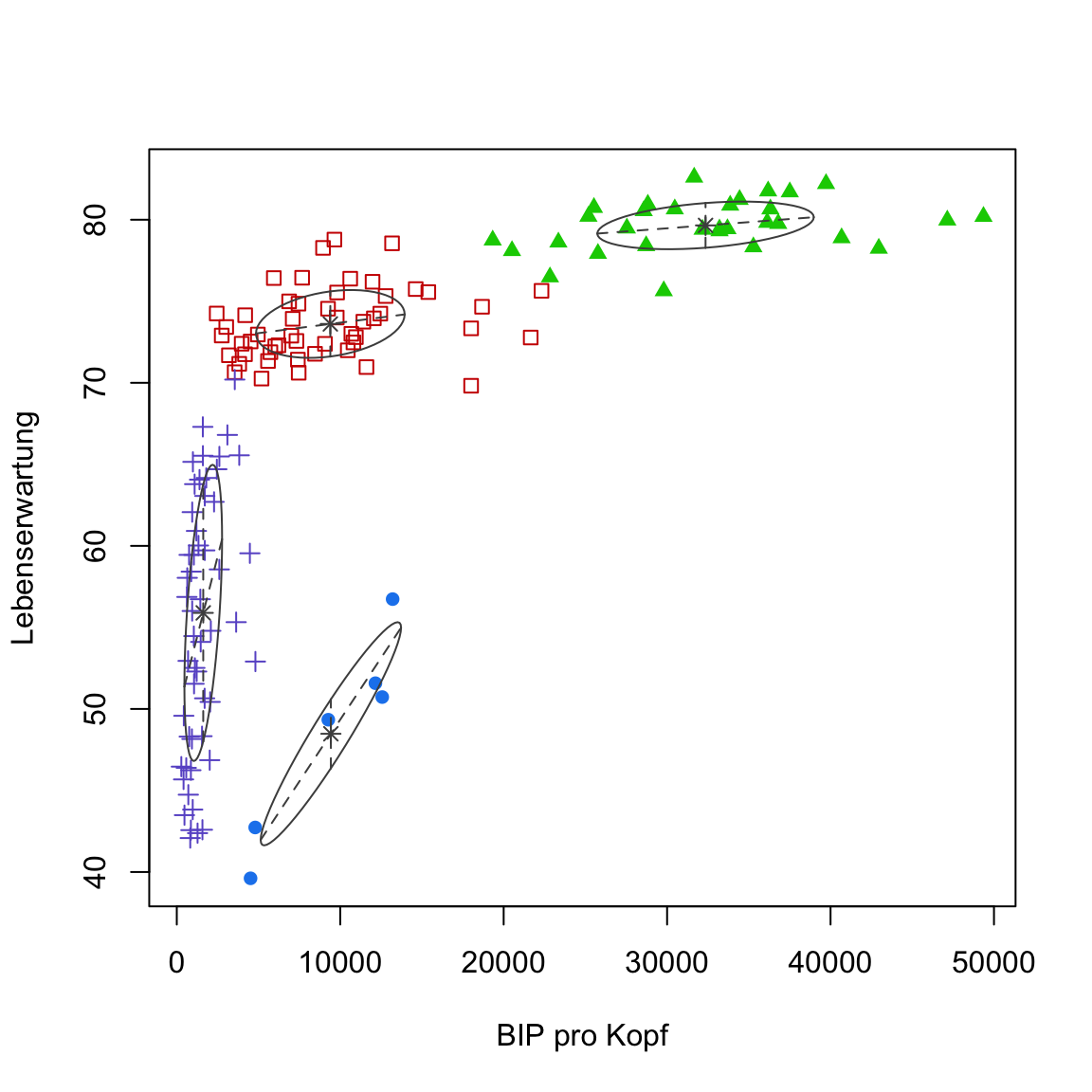

Verwende nun den Code unten um explizit nur bestimmte Gaussian Mixture Modelle zu verwenden. Verwende hierzu modelNames = 'XX' wobei ‘XX’ das Kürzel des jeweiligen Modells ist. Plotte im Anschluss die gefunden Lösungen. Probiere zunächst EEI aus. Danach spiele ein wenig herum.

# Wähle Gaussian Mixture Modell explizit aus
gap2007_gm <- Mclust(gap2007, modelNames = 'XX')
plot(gap2007_gm, what = 'classification')

# Wähle Gaussian Mixture Modell explizit aus
gap2007_gm <- Mclust(gap2007, modelNames = 'EEI')
plot(gap2007_gm, what = 'classification')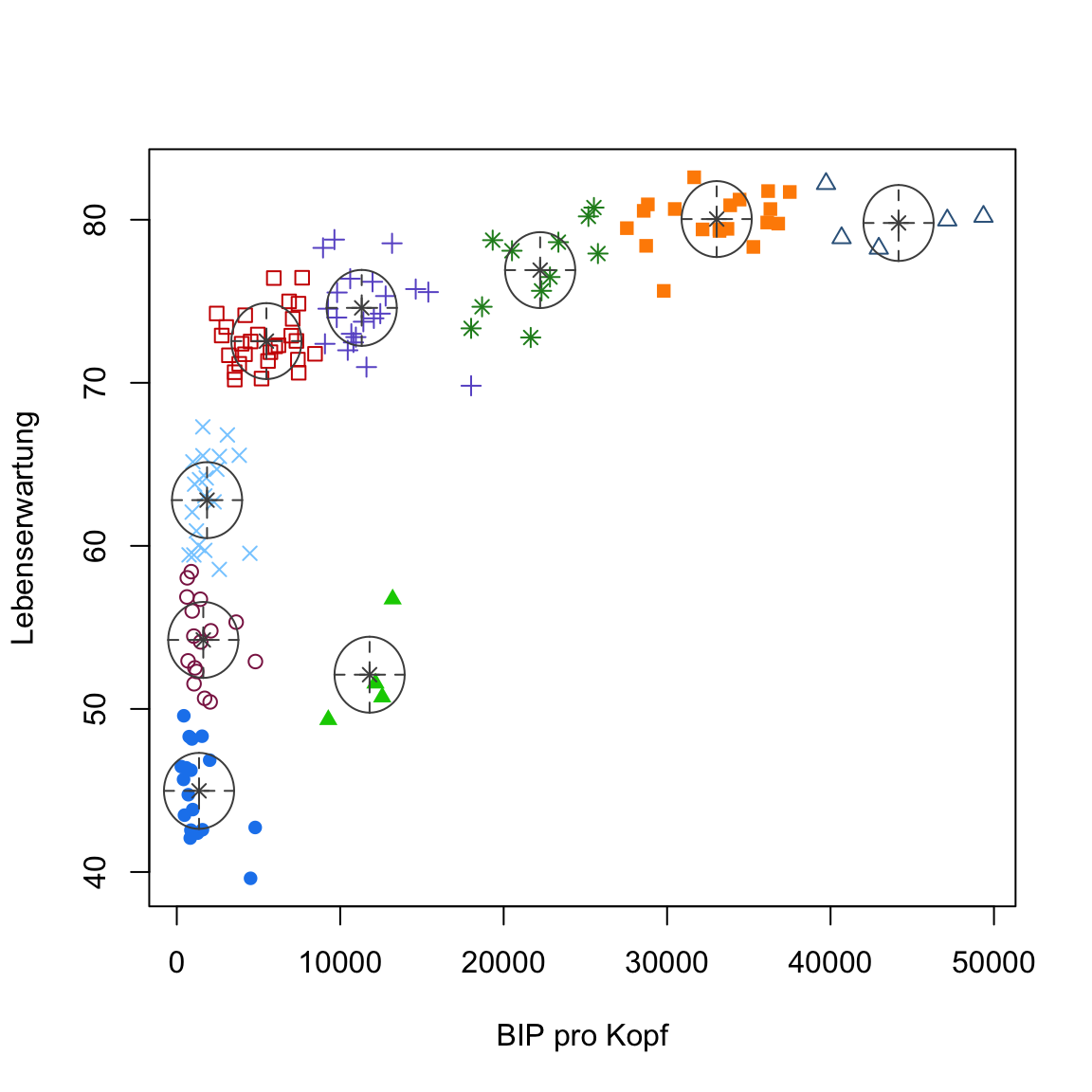

Y - Challenges: Neuer Datensatz

Verwende die read_csv() Funktion um den Datensatz credit.csv als Objekt credit einzulesen.

# Lese credit.csv
credit <- read_csv('1_Data/credit.csv')

Printe den Datensatz und verwende summary() um einen weiteren Überblick über die Daten zu bekommen.
Verwende die bis hierin geübten Methoden um zu identifizieren, ob und wie viele Cluster sich im credit Datensatz befindet. Bzw. ob und wie sich Kreditkarten Kunden in Gruppen zusammenfassen lassen. Viel Spass!

Beispiele

library(tidyverse) 
library(cstab)
library(dbscan)
library(mclust, mask.ok = F)

# Beispieldatensatz
data(mpg)

# Verarbeitung des Datensatzes
mpg <- mpg %>% select_if(is.numeric)
mpg_stand <- mpg  %>% 
  scale %>%         # Standardisieren
  as_tibble()

# k-means -----

# Finde Cluster
mpg_km <- kmeans(mpg_stand, 
                 centers = 3)

# Zeige Zentroide
mpg_km$centers

# k-selection -----

# Zeige Binnenvarianz Verlauf
km_verlauf <- purrr::map(2:20, kmeans, x = mpg_stand)
binnenvarianz <- purrr::map_dbl(km_verlauf, 
                               `[[`, i = 'tot.withinss')

# Plotte die Binnenvarianz
plot(binnenvarianz)

# Gap & Slope Statistik
k_est <- cDistance(as.matrix(mpg_stand), 
                   kseq = 2:20) 
k_est$k__Gap
k_est$k_Slope

# Cluster stability
k_est <- cStability(as.matrix(mpg_stand), 
                    kseq = 2:20) 
k_est$k_instab
  
# DBSCAN -----

# Finde Cluster
mpg_dbscan <- dbscan(mpg_stand, eps = 1)

# Zeige Zentroide
mpg %>% 
  mutate(cl = mpg_dbscan$cluster) %>%
  group_by(cl) %>% 
  summarize_all(mean)

# Gaussian Mixtures -----

# Finde Cluster
mpg_gm <- Mclust(mpg)

# Zeige Zentroide
mpg %>% 
  mutate(cl = mpg_gm$classification) %>%
  group_by(cl) %>% 
  summarize_all(mean)

# Plotte Cluster
plot(mpg_gm, what = 'classification')

# Vergleiche Cluster -----

table(mpg_km$cluster, mpg_dbscan$cluster)
table(mpg_km$cluster, mpg_gm$classification)
table(mpg_dbscan$cluster, mpg_gm$classification)

Datensätze

Datei	Zeilen	Spalten
gap.csv	1692	6
credit.csv	8636	8

gap.csv

Der gap Datensatz basiert auf dem Gapminder Projekt und stammt aus dem R Paket gapminder.

Variable	Beschreibung
Land	Name des Landes
Kontinent	Name des Kontinents
Jahr	Jahr
Lebenserwartung	in Jahren
Population	Anzahl Einwohner des Landes
BIP pro Kopf	Bruttoinlandsprodukt pro Einwohner

credit.csv

Der credit Datensatz ist ein Ausschnitt des Öffentlich verfügbaren Credit Card Dataset. Der Datensatz beinhaltet 8 Features, die einen Auschnitt des Verhaltens von 8636 Kreditkartenkunden beschreiben.

Variable	Beschreibung
BALANCE	Verfügbares Guthaben
BALANCE_FREQUENCY	Änderungsfrequenz des Guthabens (1 = häufig, 0 = selten)
PURCHASES	Summe der Einkäufe
CREDITLIMIT	Kreditlimit der Karte
ONEOFFPURCHASES	Betrag der grössten einmaligen Zahlung
MINIMUM_PAYMENTS	Minimale Konto-Ausgleichszahlung
PRCFULLPAYMENT	Prozent vollständige Konto-Ausgleichszahlung
TENURE	Dauer des Kundenverhältnisses

Funktionen

Paket

Paket	Installation
`tidyverse`	`install.packages("tidyverse")`
`cstab`	`install.packages("cstab")`
`dbscan`	`install.packages("dbscan")`
`mclust`	`install.packages("mclust")`

Funktionen

Clustering

Funktion	Paket	Beschreibung
`kmeans()`	`stats`	Clustere die Daten mit k-means
`dbscan()`	`dbscan`	Clustere die Daten mit DBSCAN
`Mclust()`	`mclust`	Clustere die Daten mit Gaussian Mixtures

k-selection

Funktion	Paket	Beschreibung
`cDistance()`	`cstab`	Identifiziere k mit distanzbasierten Methoden, z.B., der Gap Statistik.
`cStability()`	`cstab`	Identifiziere k mit stabilitätsbasierten Methoden.

Materialien

Dokumentation

Eine gutes Tutorial über k-means und hierarchisches Clustering.

Unsupervised learning

Maschinelles Lernen mit R The R Bootcamp

Überblick

Aufgaben

A - Setup

B - Lade den gap Datensatz

C - k-means

D - k-selection

E - DBSCAN

F - Gaussian Mixtures

X - Challenges: Modellselektion Gaussian mixtures

Y - Challenges: Neuer Datensatz

Beispiele

Datensätze

gap.csv

credit.csv

Funktionen

Paket

Funktionen

Materialien

Dokumentation

Maschinelles Lernen mit R
The R Bootcamp

B - Lade den `gap` Datensatz