Features

Überblick

Am Ende des Practicals wirst du wissen…

Warum Featurereduktion Sinn macht.
Wie du Features auf verschiedenen Wegen eliminieren kannst.

Aufgaben

A - Setup

Öffne dein TheRBootcamp R project.
Öffne ein neues R Skript. Schreibe deinen Namen, das Datum und “Features Practical” als Kommentare an den Anfang des Skripts.

## NAME
## DATUM
## Features Practical

Speichere das neue Skript unter dem Namen features_practical.R im 2_Code Ordner.
Lade die Pakete tidyverse, caret, party, partykit.

library(tidyverse)
library(caret)
library(party)
library(partykit)

Datensatz 1: Diabetes

B - Lade den Diabetes Datensatz

Verwende die read_csv() Funktion um diabetes.csv einzulesen.

# Lese Daten ein
diabetes <- read_csv(file = "1_Data/diabetes.csv")

Printe den Datensatz.
Verwende names(XX), summary(XX), und View() um einen weiteren Überblick über die Daten zu bekommen.
Wiederum, führe den Code unten aus um sicherzustellen, dass alle character Features als Faktoren vorliegen.

# Konvertiere alle character zu factor
diabetes <- diabetes %>% mutate_if(is.character, factor)

C - Trenne Training und Test

Bevor du irgendwas machst trenne den Datensatz in Traning und Test. Verwende createDataPartition() um zwei Datensätze diabetes_train und diabetes_test zu erstellen. Das Kriterium ist das Feature Diabetes. Dabei sollen nur 5% der Datenpunkte im Trainingsset landen. Wichtig: Setze den Random Seed auf 100 damit die Aufteilung reproduzierbar ist.

# Setze Random seed
set.seed(100)

# Index für Training
train_index <- createDataPartition(XX$XX, p = .05, list = FALSE)

# Kreiere Training- und Testdaten
diabetes_train <- XX %>% slice(train_index)
diabetes_test  <- XX %>% slice(-train_index)

# Setze Random seed
set.seed(100)

# Index für Training
train_index <- createDataPartition(diabetes$Diabetes, p = .05, list = FALSE)

# Kreiere Training- und Testdaten
diabetes_train <- diabetes %>% slice(train_index)
diabetes_test  <- diabetes %>% slice(-train_index)

D - Entferne ungewollte Features

Bevor du mit der Eliminierung der Features beginnen kannst, musst du Features und Kriterium voneinander trennen.

# Wähle Features aus
diabetes_train_pred <- diabetes_train %>% select(-XX)

# Wähle Kriterium aus
diabetes_train_crit <- diabetes_train %>% select(XX)

# Wähle Features aus
diabetes_train_pred <- diabetes_train %>% select(-Diabetes)

# Wähle Kriterium aus
diabetes_train_crit <- diabetes_train %>% select(Diabetes)

Nun teste ob es ggf. übermässig korrelierte Prädiktoren gibt. Berechne hierzu zunächst die Korrelationsmatrix mit cor(). Anschliessend übergebe diese an findCorrelation(). Gibt es Variablen die übermässig korreliert sind? Keine Werte würde nein bedeuten.

# Bestimme die Korrelationsmatrix
corr_matrix <- cor(XX_pred)

# Identifiziere übermässig korrelierte Features
findCorrelation(corr_matrix)

# Bestimmte die Korrelationsmatrix
corr_matrix <- cor(diabetes_train_pred)

# Identifiziere übermässig korrelierte Features
findCorrelation(corr_matrix)

integer(0)

Nun teste, ob es vll. Features mit limitierter “Varianz” gibt. Gibt es welche?

# Identifiziere Features ohne "Varianz"
nearZeroVar(XX_pred)

# Identifiziere Features ohne "Varianz"
nearZeroVar(diabetes_train_pred)

integer(0)

Es wurden weder übermässig korrelierte Prädiktoren gefunden, noch solche ohne “Varianz”. Füge nun Features und Kriterium wieder zu diabetes_train zusammen.

# Füge nun Features und Kriterium zusammen
diabetes_train <- XX_crit %>% bind_cols(XX_pred)

# Füge nun Features und Kriterium zusammen
diabetes_train <- diabetes_train_crit %>% bind_cols(diabetes_train_pred)

E - Featurewichtigkeit

Feature-Wichtigkeit existiert nicht für sich allein, sondern kann nur innerhalb eines Modells bestimmt werden. Fitte eine logistische Regression auf die Trainingsdaten, die das Kriterium Diabetes durch die anderen Features vorhersagt.

# Fitte Regression
diabetes_glm <- train(Diabetes ~ .,
                      data = XX,
                      method = "XX")

# Fitte Regression
diabetes_glm <- train(Diabetes ~ .,
                      data = diabetes_train,
                      method = "glm")

Berechne die Featurewichtigkeit mittels varImp(). Der Output der Funktion präsentiert in diesem Fall die t-Werte skaliert auf den Bereich 0 bis 100. Mit scale = TRUE könntest du dir die tatsächlichen t-Werte anzeigen lassen.

# Bestimme Featurewichtigkeit
varimp_glm <- varImp(XX)

# Printe Featurewichtigkeit
varimp_glm

# Plotte Featurewichtigkeit
plot(varimp_glm)

# Bestimme Featurewichtigkeit
varimp_glm <- varImp(diabetes_glm)

# Printe Featurewichtigkeit
varimp_glm

glm variable importance

                    Overall
Glucose               100.0
Alter                  57.8
fam_Vorerkrankungen    55.9
BMI                    54.7
Blutdruck              40.6
Schwangerschaften       0.0

# Plotte Featurewichtigkeit
plot(varimp_glm)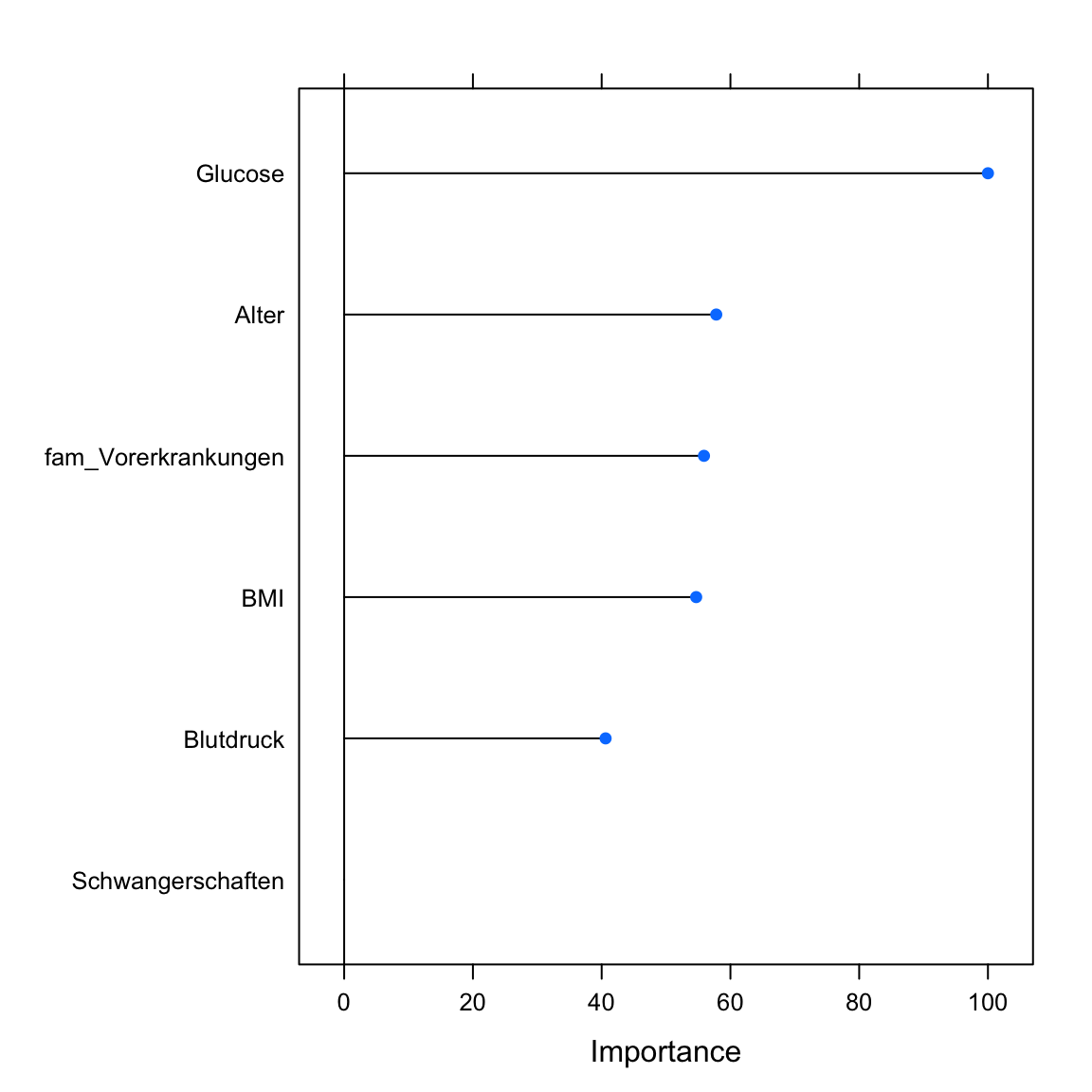

F - Modellvergleiche

Fitte nun eine zweite Regression zur Vorhersage von Diabetes, diesmal aber unter der Verwendung nur des besten Prädiktors gemäss den Ergebnissen der letzten Sektion.

# Fitte Regression mit nur dem besten Prädiktor
diabetes_glm1 <- train(diabetes ~ XX,
                       data = XX,
                       method = XX)

# Fitte Regression mit dem besten Prädiktor
diabetes_glm1 <- train(Diabetes ~ Glucose,
                       data = diabetes_train,
                       method = "glm")

Vergleiche auf die bekannte Art und Weise, wie gut die Modelle die Trainings und die Testdaten erklären. Wie unterschiedlich sind die Modelle im Traning, wie unterschiedlich im Test? Welches ist besser?

# Evaluation des Tranings
confusionMatrix(predict(XX), reference = XX)
confusionMatrix(predict(XX), reference = XX)

# Evaluation des Tests
confusionMatrix(predict(XX, newdata = XX), reference = XX)
confusionMatrix(predict(XX, newdata = XX), reference = XX)

# Evaluation des Tranings
confusionMatrix(predict(diabetes_glm), reference = diabetes_train$Diabetes)

Confusion Matrix and Statistics

          Reference
Prediction neg pos
       neg  22   1
       pos   2  12
                                        
               Accuracy : 0.919         
                 95% CI : (0.781, 0.983)
    No Information Rate : 0.649         
    P-Value [Acc > NIR] : 0.000161      
                                        
                  Kappa : 0.825         
                                        
 Mcnemar's Test P-Value : 1.000000      
                                        
            Sensitivity : 0.917         
            Specificity : 0.923         
         Pos Pred Value : 0.957         
         Neg Pred Value : 0.857         
             Prevalence : 0.649         
         Detection Rate : 0.595         
   Detection Prevalence : 0.622         
      Balanced Accuracy : 0.920         
                                        
       'Positive' Class : neg

confusionMatrix(predict(diabetes_glm1), reference = diabetes_train$Diabetes)

Confusion Matrix and Statistics

          Reference
Prediction neg pos
       neg  21   8
       pos   3   5
                                       
               Accuracy : 0.703        
                 95% CI : (0.53, 0.841)
    No Information Rate : 0.649        
    P-Value [Acc > NIR] : 0.308        
                                       
                  Kappa : 0.285        
                                       
 Mcnemar's Test P-Value : 0.228        
                                       
            Sensitivity : 0.875        
            Specificity : 0.385        
         Pos Pred Value : 0.724        
         Neg Pred Value : 0.625        
             Prevalence : 0.649        
         Detection Rate : 0.568        
   Detection Prevalence : 0.784        
      Balanced Accuracy : 0.630        
                                       
       'Positive' Class : neg

# Evaluation des Tests
confusionMatrix(predict(diabetes_glm, newdata = diabetes_test), reference = diabetes_test$Diabetes)

Confusion Matrix and Statistics

          Reference
Prediction neg pos
       neg 374  94
       pos  77 142
                                        
               Accuracy : 0.751         
                 95% CI : (0.717, 0.783)
    No Information Rate : 0.656         
    P-Value [Acc > NIR] : 5.31e-08      
                                        
                  Kappa : 0.438         
                                        
 Mcnemar's Test P-Value : 0.221         
                                        
            Sensitivity : 0.829         
            Specificity : 0.602         
         Pos Pred Value : 0.799         
         Neg Pred Value : 0.648         
             Prevalence : 0.656         
         Detection Rate : 0.544         
   Detection Prevalence : 0.681         
      Balanced Accuracy : 0.715         
                                        
       'Positive' Class : neg

confusionMatrix(predict(diabetes_glm1, newdata = diabetes_test), reference = diabetes_test$Diabetes)

Confusion Matrix and Statistics

          Reference
Prediction neg pos
       neg 378 107
       pos  73 129
                                        
               Accuracy : 0.738         
                 95% CI : (0.703, 0.771)
    No Information Rate : 0.656         
    P-Value [Acc > NIR] : 2.63e-06      
                                        
                  Kappa : 0.398         
                                        
 Mcnemar's Test P-Value : 0.0139        
                                        
            Sensitivity : 0.838         
            Specificity : 0.547         
         Pos Pred Value : 0.779         
         Neg Pred Value : 0.639         
             Prevalence : 0.656         
         Detection Rate : 0.550         
   Detection Prevalence : 0.706         
      Balanced Accuracy : 0.692         
                                        
       'Positive' Class : neg

Wahrscheinlich hast du beobachtet, dass das Modell mit vielen Prädiktoren im Test deutlich schwächer als im Traning war, aber auch, dass es immer noch leicht besser als das Modell mit nur einem Prädiktor war. Unter welchen Bedingungen würdest du erwarten, dass das Modell mit nur einem Prädiktor die Oberhand im Test erhält?

Datensatz 2: Murders

G - Lade den Murders Datensatz

Verwende die read_csv() Funktion um murders_crime.csv einzulesen.

# Lese Daten ein
murders <- read_csv(file = "1_Data/murders_crime.csv")

Printe den Datensatz.
Verwende names(XX), summary(XX), und View() um einen weiteren Überblick über die Daten zu bekommen.
Führe den Code unten aus um sicherzustellen, dass alle character Features als Faktoren vorliegen.

# Konvertiere alle character zu factor
murders <- murders %>% mutate_if(is.character, factor)

H - Trenne Training und Test

Trenne den Datensatz in Traning und Test. Verwende createDataPartition() um zwei Datensätze murders_train und murders_test zu erstellen. Das Kriterium ist murders. Dabei sollen nur 25% der Datenpunkte im Trainingsset landen. Wichtig: Setze den Random Seed auf 100 damit die Aufteilung reproduzierbar ist.

# Setze Random seed
set.seed(100)

# Index für Training
train_index <- createDataPartition(XX$XX, p = .25, list = FALSE)

# Kreiere Training- und Testdaten
murders_train <- XX %>% slice(train_index)
murders_test  <- XX %>% slice(-train_index)

# Setze Random seed
set.seed(100)

# split index
train_index <- createDataPartition(murders$murders, p = .25, list = FALSE)

# train and test sets
murders_train <- murders %>% slice(train_index)
murders_test  <- murders %>% slice(-train_index)

I - Entferne ungwollte Features

Bevor du mit der Eliminierung der Features beginnst, trenne Features und Kriterium voneinander.

# Wähle Features aus
murders_train_pred <- murders_train %>% select(-XX)

# Wähle Kriterium aus
murders_train_crit <- murders_train %>% select(XX)

# Wähle Features aus
murders_train_pred <- murders_train %>% select(-murders)

# Wähle Kriterium aus
murders_train_crit <- murders_train %>% select(murders)

Nun teste ob es ggf. übermässig korrelierte Prädiktoren gibt. Berechne hierzu zunächst die Korrelationsmatrix mit cor(). Anschliessend übergebe diese an findCorrelation(). Gibt es Variablen die übermässig korreliert sind? Keine Werte würde nein bedeuten.

# Bestimmte die Korrelationsmatrix
corr_matrix <- cor(XX_pred)

# Identifiziere übermässig korrelierte Features
findCorrelation(corr_matrix)

# Bestimmte die Korrelationsmatrix
corr_matrix <- cor(murders_train_pred)

# Identifiziere übermässig korrelierte Features
findCorrelation(corr_matrix)

 [1]  8 11 17 27 30 41 44 49 53 54 55 57 58 59 60 61 64 65 71 80 81 84 85 87 91
[26]  7 14 13 20 21 31 38 43  1 62 67 51

Verwende den Code unten um die übermässig korrelierten Features zu entfernen.

# Entferne korrelierte Features
murders_train_pred <- murders_train_pred %>% select(-findCorrelation(corr_matrix))

Nun teste, ob es Prädiktoren mit limitierter “Varianz” gibt. Gibes es welche?

# Identifiziere Features ohne "Varianz"
nearZeroVar(XX_pred)

# Identifiziere Features ohne "Varianz"
nearZeroVar(murders_train_pred)

integer(0)

Verwende den code unten um die Prädiktoren ohne “Varianz” zu entfernen.

# Entferne Features ohne Varianz
murders_train_pred <- murders_train_pred %>% select(-nearZeroVar(murders_train_pred))

Füge nun Features und Kriterium als neuen Trainingsdatensatz murders_train_reduziert zusammen.

# Füge nun Features und Kriterium zusammen
murders_train_reduziert <- XX_crit %>% bind_cols(XX_pred)

# Füge nun Features und Kriterium zusammen
murders_train_reduziert <- murders_train_crit %>% bind_cols(murders_train_pred)

J - Featurewichtigkeit

Fitte eine logistische Regression auf die reduzierten Traningsdaten murders_train_reduziert, die das Feature murders durch die anderen Feature vorhersagt.

# Fitte Regression
murders_glm_reduziert <- train(murders ~ .,
                               data = XX,
                               method = "XX")

# Fitte Regression
murders_glm_reduziert <- train(murders ~ .,
                               data = murders_train_reduziert,
                               method = "glm")

Berechne und Plotte die Featurewichtigkeit mittels varImp().

# Bestimme Featurewichtigkeit
varimp_glm <- varImp(XX)

# Printe Featurewichtigkeit
varimp_glm

# Plotte Featurewichtigkeit
plot(varimp_glm)

# Bestimme Featurewichtigkeit
varimp_glm <- varImp(murders_glm_reduziert)

# Printe Featurewichtigkeit
varimp_glm

glm variable importance

  only 20 most important variables shown (out of 64)

                    Overall
LandArea              100.0
PctBornSameState       73.5
PopDens                57.9
PctSameState85         51.2
pctWInvInc             49.6
racepctblack           47.8
FemalePctDiv           47.8
PctKidsBornNeverMar    45.6
MedNumBR               44.9
LemasPctOfficDrugUn    44.7
PctUsePubTrans         44.6
MedRentPctHousInc      43.2
agePct16t24            42.8
PctUnemployed          40.0
PersPerFam             37.3
racePctAsian           35.9
MalePctNevMarr         35.7
PctWOFullPlumb         34.8
OwnOccLowQuart         32.0
PctLess9thGrade        31.9

# Plotte Featurewichtigkeit
plot(varimp_glm)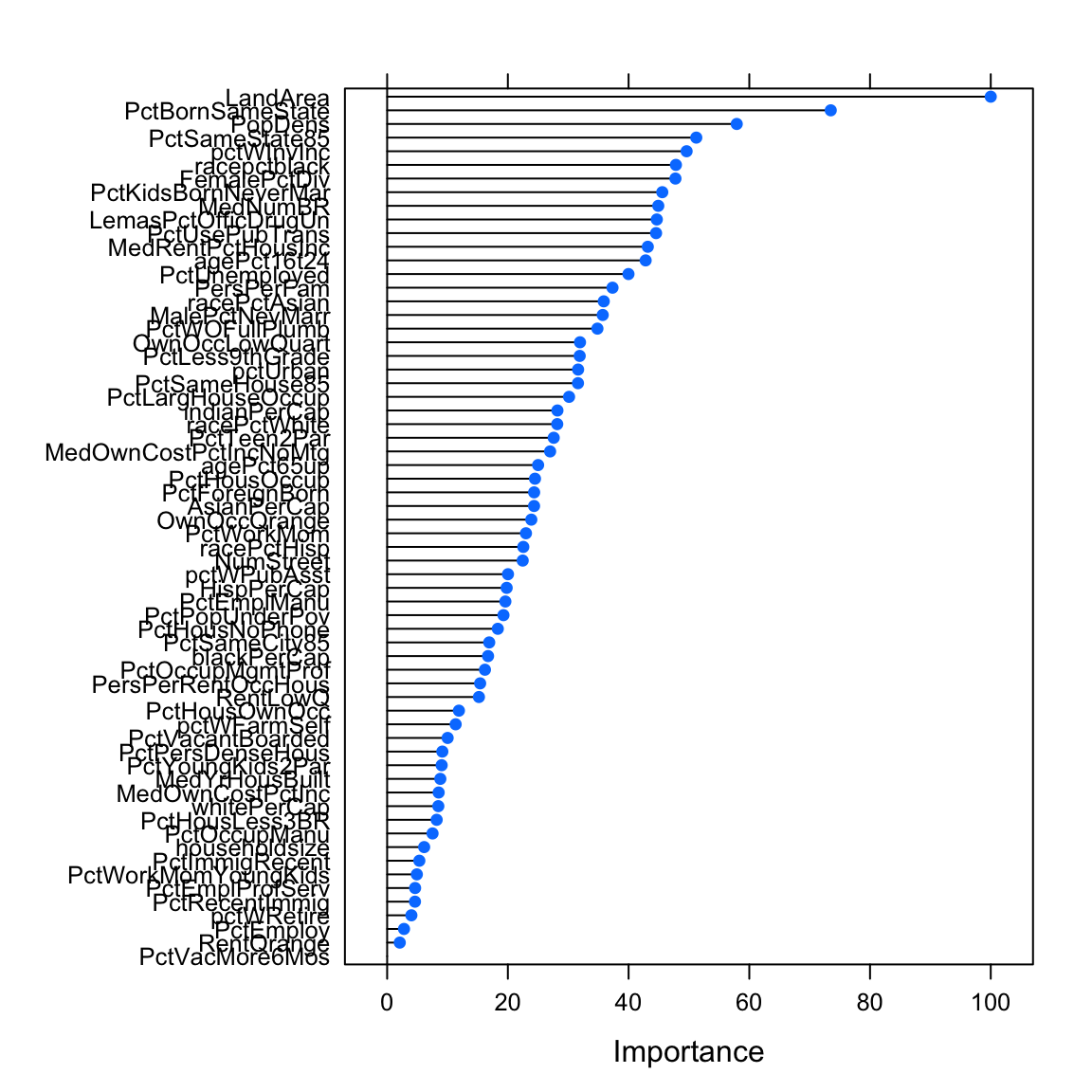

Benutze den folgenden Code um zwei neue Trainingsdatensätze zu generieren, einen der nur Features mit Importance > 50 und einen der nur Features mit Importance > 30 enthält.

# Features mit Imp > 50
murders_train_reduziert50 <- murders_train_reduziert %>% 
  select(1, which(varimp_glm$importance > 50) + 1)

# Features mit Imp > 30
murders_train_reduziert30 <- murders_train_reduziert %>% 
  select(1, which(varimp_glm$importance > 30) + 1)

K - Datenkomprimierung mit PCA

Eine Alternative zu manueller Featurereduktion ist die principal component analysis. Fitte zwei Regressionsmodelle, die murders durch die anderen Features vorhersagen unter Verwendung des Arguments preProcess = c("pca"). Zusätzlich verwende das trControl Argument um festzulegen, wie viel Varianz durch die PCA aufgeklärt werden soll. Siehe Code.

# Fitte Regression mit 80% Varianz präserviert
murders_glm_pca80 = train(murders ~ .,
                          data = murders_train,
                          method = "glm",
                          preProcess = c("pca"),
                          trControl = trainControl(preProcOptions = list(thresh = .8)))

# Fitte Regression mit 50% Varianz präserviert
murders_glm_pca50 = train(murders ~ .,
                          data = murders_train,
                          method = "glm",
                          preProcess = c("pca"),
                          trControl = trainControl(preProcOptions = list(thresh = .5)))

L - Modellvergleiche

Fitte jeweils eigene Regressionsmodelle unter Verwendung des ursprünglichen Trainingsdatensatzes murders_train und den Trainingsdatensätzen murders_train_reduziert50 und murders_train_reduziert30.

# Fitte Regression mit reduziertem Datensatz
murders_glm <- train(murders ~ .,
                     data = murders_train,
                     method = "glm")

# Fitte Regression mit reduziertem Datensatz mit Features mit Imp > 50
murders_glm_reduziert50 <- train(murders ~ .,
                               data = murders_train_reduziert50,
                               method = "glm")

# Fitte Regression mit reduziertem Datensatz mit Features mit Imp > 20
murders_glm_reduziert30 <- train(murders ~ .,
                               data = murders_train_reduziert30,
                               method = "glm")

Vergleiche die Modelle murders_glm, murders_glm_reduziert, murders_glm_reduziert50, murders_glm_reduziert30, murders_glm_pca80, murders_glm_pca50 in ihrer Fähigkeit die Testdaten vorherzusagen. Waren die Strategien der Featurereduktion erfolgreich? Welche Strategien waren am erfolgreichsten?

# Evaluation des Tests für murders_glm
confusionMatrix(predict(murders_glm, 
                        newdata = murders_test), 
              reference = murders_test$murders)

Confusion Matrix and Statistics

          Reference
Prediction  no yes
       no  430 187
       yes 200 550
                                        
               Accuracy : 0.717         
                 95% CI : (0.692, 0.741)
    No Information Rate : 0.539         
    P-Value [Acc > NIR] : <2e-16        
                                        
                  Kappa : 0.429         
                                        
 Mcnemar's Test P-Value : 0.542         
                                        
            Sensitivity : 0.683         
            Specificity : 0.746         
         Pos Pred Value : 0.697         
         Neg Pred Value : 0.733         
             Prevalence : 0.461         
         Detection Rate : 0.315         
   Detection Prevalence : 0.451         
      Balanced Accuracy : 0.714         
                                        
       'Positive' Class : no

# Evaluation des Tests für murders_glm_reduziert
confusionMatrix(predict(murders_glm_reduziert, 
                        newdata = murders_test), 
                reference = murders_test$murders)

Confusion Matrix and Statistics

          Reference
Prediction  no yes
       no  471 187
       yes 159 550
                                       
               Accuracy : 0.747        
                 95% CI : (0.723, 0.77)
    No Information Rate : 0.539        
    P-Value [Acc > NIR] : <2e-16       
                                       
                  Kappa : 0.492        
                                       
 Mcnemar's Test P-Value : 0.147        
                                       
            Sensitivity : 0.748        
            Specificity : 0.746        
         Pos Pred Value : 0.716        
         Neg Pred Value : 0.776        
             Prevalence : 0.461        
         Detection Rate : 0.345        
   Detection Prevalence : 0.481        
      Balanced Accuracy : 0.747        
                                       
       'Positive' Class : no

# Evaluation des Tests für murders_glm_reduziert50
confusionMatrix(predict(murders_glm_reduziert50, 
                        newdata = murders_test), 
                reference = murders_test$murders)

Confusion Matrix and Statistics

          Reference
Prediction  no yes
       no  403 255
       yes 227 482
                                        
               Accuracy : 0.647         
                 95% CI : (0.621, 0.673)
    No Information Rate : 0.539         
    P-Value [Acc > NIR] : 3.21e-16      
                                        
                  Kappa : 0.293         
                                        
 Mcnemar's Test P-Value : 0.219         
                                        
            Sensitivity : 0.640         
            Specificity : 0.654         
         Pos Pred Value : 0.612         
         Neg Pred Value : 0.680         
             Prevalence : 0.461         
         Detection Rate : 0.295         
   Detection Prevalence : 0.481         
      Balanced Accuracy : 0.647         
                                        
       'Positive' Class : no

# Evaluation des Tests für murders_glm_reduziert30
confusionMatrix(predict(murders_glm_reduziert30, 
                        newdata = murders_test), 
                reference = murders_test$murders)

Confusion Matrix and Statistics

          Reference
Prediction  no yes
       no  469 198
       yes 161 539
                                        
               Accuracy : 0.737         
                 95% CI : (0.713, 0.761)
    No Information Rate : 0.539         
    P-Value [Acc > NIR] : <2e-16        
                                        
                  Kappa : 0.474         
                                        
 Mcnemar's Test P-Value : 0.0574        
                                        
            Sensitivity : 0.744         
            Specificity : 0.731         
         Pos Pred Value : 0.703         
         Neg Pred Value : 0.770         
             Prevalence : 0.461         
         Detection Rate : 0.343         
   Detection Prevalence : 0.488         
      Balanced Accuracy : 0.738         
                                        
       'Positive' Class : no

# Evaluation des Tests für murders_glm_pca80
confusionMatrix(predict(murders_glm_pca80, 
                        newdata = murders_test), 
                reference = murders_test$murders)

Confusion Matrix and Statistics

          Reference
Prediction  no yes
       no  506 186
       yes 124 551
                                       
               Accuracy : 0.773        
                 95% CI : (0.75, 0.795)
    No Information Rate : 0.539        
    P-Value [Acc > NIR] : < 2e-16      
                                       
                  Kappa : 0.547        
                                       
 Mcnemar's Test P-Value : 0.000531     
                                       
            Sensitivity : 0.803        
            Specificity : 0.748        
         Pos Pred Value : 0.731        
         Neg Pred Value : 0.816        
             Prevalence : 0.461        
         Detection Rate : 0.370        
   Detection Prevalence : 0.506        
      Balanced Accuracy : 0.775        
                                       
       'Positive' Class : no

# Evaluation des Tests für murders_glm_pca50
confusionMatrix(predict(murders_glm_pca50, 
                        newdata = murders_test), 
                reference = murders_test$murders)

Confusion Matrix and Statistics

          Reference
Prediction  no yes
       no  467 195
       yes 163 542
                                        
               Accuracy : 0.738         
                 95% CI : (0.714, 0.761)
    No Information Rate : 0.539         
    P-Value [Acc > NIR] : <2e-16        
                                        
                  Kappa : 0.475         
                                        
 Mcnemar's Test P-Value : 0.101         
                                        
            Sensitivity : 0.741         
            Specificity : 0.735         
         Pos Pred Value : 0.705         
         Neg Pred Value : 0.769         
             Prevalence : 0.461         
         Detection Rate : 0.342         
   Detection Prevalence : 0.484         
      Balanced Accuracy : 0.738         
                                        
       'Positive' Class : no

X - Challenges: Violent & Non-violent Crime Data

Versuche neue Trainingsdatensätze unter Verwendung manueller Reduktion oder PCA zu generieren die zu noch besseren Vorhersagen führen.
Verwende Random Forest anstatt Regression als zugrundeliegendes Modell. Achte darauf, dass mtry nicht zu hoch ist, damit es nicht so lange dauert.
Für die Datensätze violent_crime.csv und nonviolent_crime.csv modelliere ViolentCrimesPerPop respektive nonViolPerPop als Funktion einer sinnvollen Auswahl an Featuren. Beide Kriterien sind numerisch, was bedeutet, dass es sich hier um ein Regressionsproblem handelt.

Beispiele

# Schritt 0: Pakete laden-----------

library(tidyverse)   
library(caret)   
library(party)
library(partykit)

# Schritt 1: Lade Daten ----------------------

# Lese Daten
data <- mpg

# Konvertiere character in factor
data <- data %>%
  mutate_if(is.character, factor)


# Schritt 2: Kreiere Training und Test -------------

# Kreiere Trainingsindex
train_index <- createDataPartition(criterion, 
                                   p = .8, 
                                   list = FALSE)

# Kreiere Training und Test
data_train <- data %>% slice(train_index)
data_test <- data %>% slice(-train_index)

# Trenne Features und Kriterium
criterion_train <- data_train %>% select(hwy) %>% pull()
predictors_train <- data_train %>% select(-hwy)
criterion_test <- data_test %>% select(hwy) %>% pull()
predictors_test <- data_test %>% select(-hwy)

# Schritt 3: Bereinige Daten -------------

# Teste auf Multikollinearität
corr_matrix <- cor(predictors_train)
corr_features <- findCorrelation(corr_matrix)

# Entferene exzessiv korrelierte Feature
predictors_train <- predictors_train %>% select(-corr_features)

# Teste auf zu wenig "Varianz"
zerovar_features <- nearZeroVar(predictors_train)

# Entferene Feature mit zu wenig "Varianz"
predictors_train <- predictors_train %>% select(-zerovar_features)

# Verbinde Prädiktoren und Kriterium
data_train <- predictors_train %>% add_column(hwy = criterion_train)

# Schritt 4: Definiere Kontrollparameter -------------

# Trainiere mittels Cross-Validation
ctrl_cv <- trainControl(method = "cv") 

# Schritt 5: Fitte die Modelle -------------

# Fitte vanilla flavor Regression
hwy_glm <- train(form = hwy ~ .,
                 data = data_train,
                 method = "glm",
                 trControl = ctrl_cv)

# Fitte mit PCA transformation
hwy_glm_pca <- train(form = hwy ~ .,
                     data = data_train,
                     method = "glm",
                     trControl = ctrl_cv,
                     preProcess = c('pca'))

# Fitte mit Standardisierung
hwy_glm_sca <- train(form = hwy ~ .,
                     data = data_train,
                     method = "glm",
                     trControl = ctrl_cv,
                     preProcess = c('scale', 'center'))

# Extrahiere fits
glm_fit     <- predict(hwy_glm)
glm_pca_fit <- predict(hwy_glm_pca)
glm_sca_fit <- predict(hwy_glm_sca)

# Schritt 6: Evaluiere die Featurewichtigkeiet -------------

# Berechne Wichtigkeit
imp_glm     <- varImp(hwy_glm)
imp_glm_pca <- varImp(hwy_glm_pca)
imp_glm_sca <- varImp(hwy_glm_sca)

# Plotte Wichtigkeit
plot(imp_glm)
plot(imp_glm_pca)
plot(imp_glm_sca)

# Schritt 7: Wähle Variablen aus -------------

# Per Hand
hwy_glm_sel <- train(form = hwy ~ cty,
                     data = data_train,
                     method = "glm",
                     trControl = ctrl_cv)

# Setze PCA Varianz auf 50%
ctrl_cv_pca <- trainControl(method = "cv",
                            preProcOptions = list(thresh = 0.50)) 

# Modell mit PCA mit 50% Varianz
hwy_glm_sel <- train(form = hwy ~ .,
                     data = data_train,
                     method = "glm",
                     trControl = ctrl_cv_pca,
                     preProcess = c('pca'))

# Schritt 8: Rekursive Featurerediktion -------------

# RFE Einstellungen 
ctrl_rfe <- rfeControl(functions = lmFuncs,  # linear model
                       method = "cv",
                       verbose = FALSE)

# RFE
profile <- rfe(x = predictors_train, 
               y = criterion_train,
               sizes = c(1, 2, 3),    # Kandidaten
               rfeControl = ctrl_rfe)

# Plotte Ergebnisse
trellis.par.set(caretTheme())
plot(profile, type = c("g", "o"))

# Schritt 9: Evaluiere die Modelle -------------

# Ihr wisst wie...

Datensätze

Datei	Zeilen	Spalten
diabetes.csv	724	7
murders_crime.csv	1000	102
violent_crime.csv	1000	102
nonviolent_crime.csv	1000	102

`diabetes`

Der diabetes Datensatz entstammt dem PimaIndiansDiabetes Datensatz aus dem mlbench Paket. Er beinhaltet medizinische und demographische Daten der Pima.

Die Pima sind eine in Arizona lebende Untergruppe der Indianer. Eine genetische Prädisposition erlaubte es ihnen sich jahrelang von einer sehr kohlenhydratarmen Diät zu ernähren. Der Wechsel von traditionellem Anbau zu industriell verarbeiteten Nahrungsmitteln zusammen mit einem Rückgang physischer Aktivität hat bei den Pima zu einer sehr hohen Rate and Typ 2 Diabetes geführt. Aus diesem Grund sind sie Gegenstand vieler medizinischer Untersuchungen.

Name	Beschreibung
Diabetes	Diagnose: positiv (pos) oder negativ (pos)
Schwangerschaften	Anzahl Schwangerschaften
Glucose	Glukosekonzentration im Plasma
Blutdruck	Diastolischer Blutdruck
BMI	Body Mass Index
fam_Vorerkrankungen	Familiäre Vorerkrankungen (pedigree function)
Alter	Alter in Jahren

`murders_crime`, `violent_crime`, und `non_violent_crime`

Die Datensätze murders_crime, violent_crime, und non_violent_crime entstammen dem Communities and Crime Unnormalized Data Set aus dem UCI Machine Learning Repository. Für die Featurebeschreibungen siehe: Communities and Crime Unnormalized Data Set. Aufgrund der grossen Anzahl der Feature (102) verzichten wir auf hier auf die Tabelle.

Der Datensatz kombiniert sozio-demographische Daten des US 1990 Zensus, Daten aus dem Law Enforcement Management and Admin Stats Survey, und Kriminaldaten des FBI.

Funktionen

Pakete

Paket	Installation
`tidyverse`	`install.packages("tidyverse")`
`caret`	`install.packages("caret")`
`partykit`	`install.packages("partykit")`
`party`	`install.packages("party")`

Funktionen

Funktion	Paket	Beschreibung
`trainControl()`	`caret`	Definiere wie das Modell trainiert wird
`train()`	`caret`	Trainiere (fitte) ein Modell
`predict(object, newdata)`	`stats`	Vorhersage des Kriteriumswerts in `newdata`
`postResample()`	`caret`	Evaluiere Performanz in Regressionsfällen
`confusionMatrix()`	`caret`	Evaluiere Performanz in Klassifikationsfällen
`varImp()`	`caret`	Determiniere modellspezifische, wichtige Features
`findCorrelation()`, `nearZeroVar()`	`caret`	Identifiziere hochkorrelierte Features und Features mit fast keiner Varianz.
`rfe()`, `rfeControl()`	`caret`	Verwende und kontrolliere rekursive Featureselektion.

Materialien

Cheatsheet

Features

Maschinelles Lernen mit R The R Bootcamp

Überblick

Aufgaben

A - Setup

B - Lade den Diabetes Datensatz

C - Trenne Training und Test

D - Entferne ungewollte Features

E - Featurewichtigkeit

F - Modellvergleiche

G - Lade den Murders Datensatz

H - Trenne Training und Test

I - Entferne ungwollte Features

J - Featurewichtigkeit

K - Datenkomprimierung mit PCA

L - Modellvergleiche

X - Challenges: Violent & Non-violent Crime Data

Beispiele

Datensätze

diabetes

murders_crime, violent_crime, und non_violent_crime

Funktionen

Pakete

Funktionen

Materialien

Cheatsheet

Maschinelles Lernen mit R
The R Bootcamp

`diabetes`

`murders_crime`, `violent_crime`, und `non_violent_crime`