Optimizing

Überblick

In diesem Practical wirst du optimale Tuning Parameter identifizieren für eine bestmögliche Vorhersageperformanz.

Am Ende des Practicals wirst du wissen wie man…

Cross-Validation zur Auswahl der Tuning Parameter verwendet.
Wie sich eine simple Regression von Lasso und Ridge unterscheidet.

Aufgaben

A - Setup

Öffne dein TheRBootcamp R project.
Öffne ein neues R Skript. Schreibe deinen Namen, das Datum und “Optimizing Practical” als Kommentare an den Anfang des Skripts.

## NAME
## DATUM
## Optimizing Practical

Speichere das neue Skript unter dem Namen optimizing_practical.R im 2_Code Ordner.
Lade die Pakete tidyverse, caret, party, partykit.

library(tidyverse)
library(caret)
library(party)
library(partykit)

B - Lade die `baseball` Datensätze

Verwende die read_csv() Funktion um die Datensätze baseball_train.csv und baseball_test.csv einzulesen.

# Lese Daten ein
baseball_train <- read_csv(file = "1_Data/baseball_train.csv")
baseball_test <- read_csv(file = "1_Data/baseball_test.csv")

Printe die Datensätze.
Verwende names(XX), summary(XX), und View(XX) um einen weiteren Überblick über die Daten zu bekommen.
Wiederum, führe den Code unten aus um sicherzustellen, dass alle character Features als Faktoren vorliegen.

# Konvertiere alle character zu factor
baseball_train <- baseball_train %>%
          mutate_if(is.character, factor)

baseball_test <- baseball_test %>%
          mutate_if(is.character, factor)

C - Definiere `trainControl`

Definiere ein Objekt ctrl_cv das 10-fold Cross-Validation als Resampling Methode bestimmt. Im Detail,…

setze das method Argument auf "cv" für Cross-Validation.
setze das number Argument auf 10 für 10 folds.

# Verwende 10-fold Cross-Validation
ctrl_cv <- trainControl(method = "XX", 
                        number = XX)

# Verwende 10-fold Cross-Validation
ctrl_cv <- trainControl(method = "cv", 
                        number = 10)

C - Regression

Fitte eine normale Regression auf bekanntem Wege (z.B. wie im Practical zu Prediction), die das Gehalt des Baseballspielers durch alle Features im Datensatz vorhersagt. Einziger Unterschied: Setze das trControl Argument auf das eben definierte ctrl_cv Objekt.

# Normal Regression
gehalt_glm <- train(form = XX ~ .,
                    data = XX,
                    method = "XX",
                    trControl = XX)

# Normal Regression
gehalt_glm <- train(form = Gehalt ~ .,
                   data = baseball_train,
                   method = "glm",
                   trControl = ctrl_cv)

Exploriere gehalt_glm indem du gehalt_glm$finalModel printest und summary() auf das Fit-Objekt anwendest. Wie beurteilst du die Outputs?

gehalt_glm

Generalized Linear Model 

213 samples
 19 predictor

No pre-processing
Resampling: Cross-Validated (10 fold) 
Summary of sample sizes: 192, 191, 191, 192, 191, 192, ... 
Resampling results:

  RMSE  Rsquared  MAE
  312   0.528     229

D - Ridge Regression

Bevor du ein Regressionsmodel mit Ridge fitten kannst, benötigst du das Kandidatenset für die Tuning Parameter. Erstelle hierzu mit dem Code einen Vector von möglichen lambda Werten.

# Kandidaten für lambda
lambda_vec <- 10 ^ (seq(-4, 4, length = 100))

Fitte eine Ridge Regression, die das Gehalt des Baseballspielers durch alle Feature im Datensatz vorhersagt. Hierzu kannst du mit dem Code der normalen Regression beginnen und anschliessend zwei Änderungen vornehmen:

setze das preProcess Argument auf c("center", "scale") um möglichen Problemen mit unterschielichen Skalierungen aus dem Weg zu gehen, die bei Regularisierung auftreten können.
setze das tuneGrid auf expand.grid(alpha = 0, lambda = lambda_vec) um Ridge auszuwählen und alle verschiedenen Kandidaten in lambda_vec durchlaufen zu lassen.

# Ridge Regression
gehalt_ridge <- train(form = XX ~ .,
                      data = XX,
                      method = "XX",
                      trControl = XX,
                      preProcess = XX,  
                      tuneGrid = XX)

# Ridge Regression
gehalt_ridge <- train(form = Gehalt ~ .,
                      data = baseball_train,
                      method = "glmnet",
                      trControl = ctrl_cv,
                      preProcess = c("center", "scale"), 
                      tuneGrid = expand.grid(alpha = 0, 
                                             lambda = lambda_vec))

Plotte das Objekt gehalt_ridge mit plot(). Was verrät dir der Plot? Welcher lambda Wert könnte optimal sein?

plot(gehalt_ridge)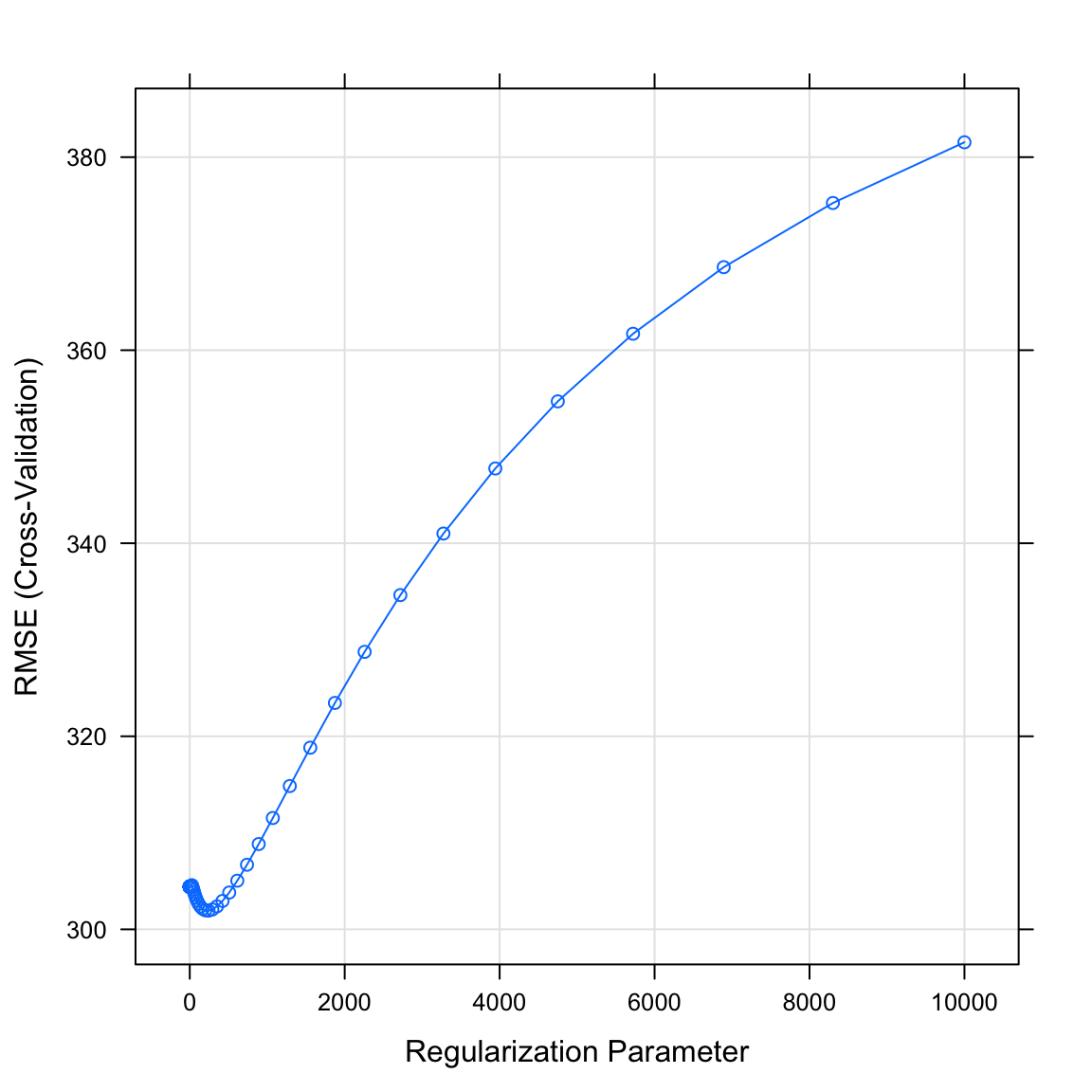

Printe mit dem Code unten den durch die Cross-Validation als bestes lambda identifizierten Wert. Passt er zum Plot in der letzten Aufgabe?

# Printe besten lambda parameter
gehalt_ridge$bestTune$lambda

[1] 242

Lasse dir mit dem Code unten die Parameter des finale Modells anzeigen. Wie beurteilst du den Output?

# Erhalte die Modellparameter für das Modell unter dem optimalen lambda
coef(gehalt_ridge$finalModel, 
     gehalt_ridge$bestTune$lambda)

20 x 1 sparse Matrix of class "dgCMatrix"
                    1
(Intercept)   518.822
Schlaeger86    19.721
Getroffen86    50.952
Home_runs86     3.052
Runs86         30.331
Runs_andere86  20.753
Walks86        41.547
Putout86       55.907
Vorlage86     -16.550
Fehler86       -8.857
Erfahrung       9.199
Schlaeger      22.937
Getroffen      38.660
Home_runs      38.065
Runs           37.822
Runs_andere    40.529
Walks           5.158
LigaN          -0.234
DivisionW     -38.463
Liga87N         1.474

E - Lasso Regression

Fitte eine Lasso Regression, die das Gehalt des Baseballspielers durch alle Features im Datensatz vorhersagt. Beginne mit dem Code für die Ridge Regression und definiere als einzige Änderung alpha = 1.

# Fit a lasso regression
gehalt_lasso <- train(form = Gehalt ~ .,
                   data = baseball_train,
                   method = "glmnet",
                   trControl = ctrl_cv,
                   preProcess = c("center", "scale"),
                   tuneGrid = expand.grid(alpha = 1,  # Lasso penalty
                                          lambda = lambda_vec))

Plotte das Objekt gehalt_lasso mit plot(). Was verrät dir der Plot? Welcher lambda Wert könnte optimal sein?

plot(gehalt_lasso)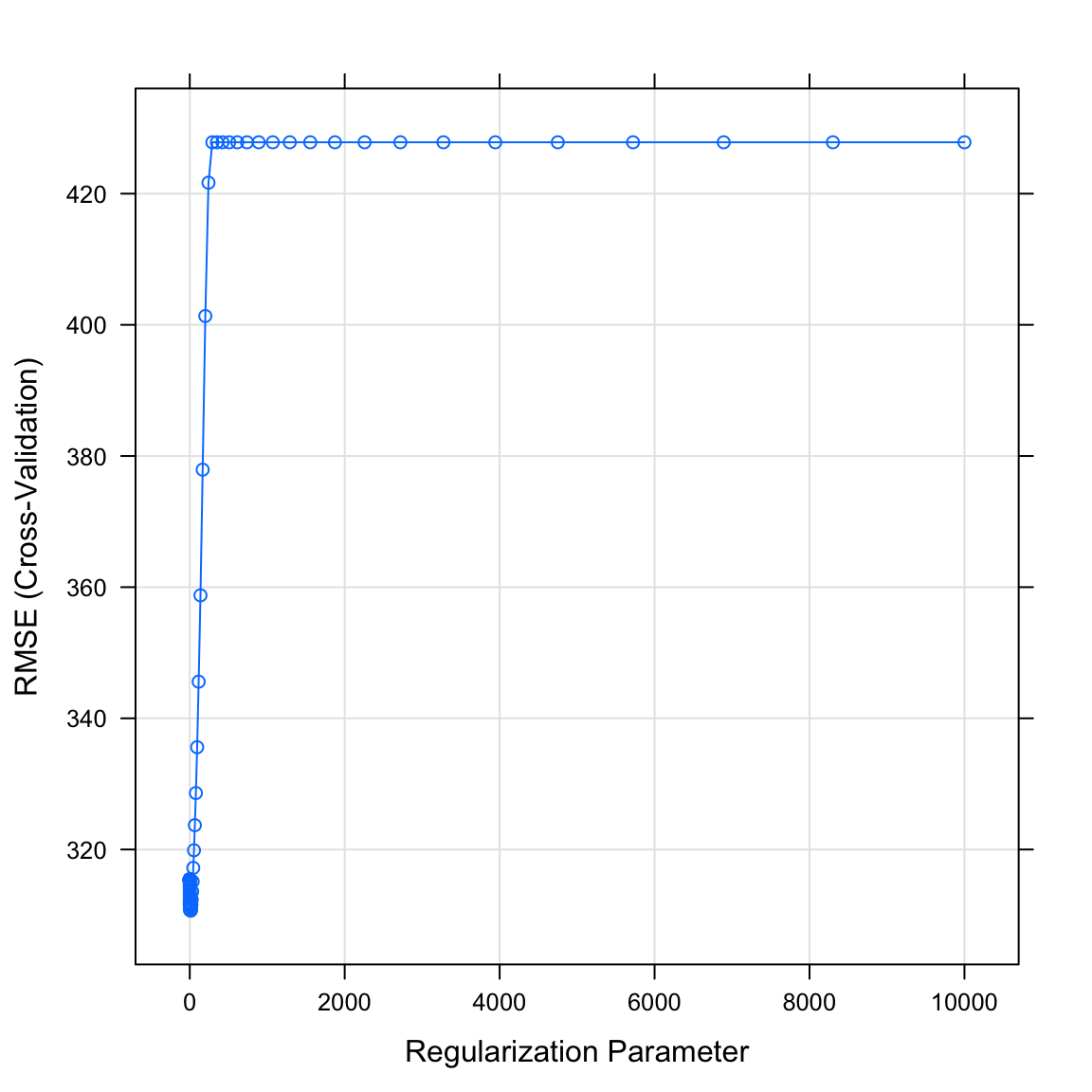

Printe mit dem Code unten den durch die Cross-Validation als bestes lambda identifizierten Wert. Passt er zum Plot in der letzten Aufgabe?

# Printe besten lambda Parameter
gehalt_lasso$bestTune$lambda

[1] 12.3

Lasse dir mit dem Code unten die Parameter des finalen Modells anzeigen. Wie beurteilst du den Output? Hat sich was im Vergleich zu Ridge verändert?

# Erhalte die Modellparameter für das Modell unter dem optimalen lambda
coef(gehalt_lasso$finalModel, 
     gehalt_lasso$bestTune$lambda)

20 x 1 sparse Matrix of class "dgCMatrix"
                  1
(Intercept)   518.8
Schlaeger86     .  
Getroffen86   116.5
Home_runs86     .  
Runs86          .  
Runs_andere86   .  
Walks86        49.8
Putout86       70.2
Vorlage86     -24.5
Fehler86        .  
Erfahrung       .  
Schlaeger       .  
Getroffen       .  
Home_runs      25.3
Runs           71.8
Runs_andere   102.2
Walks           .  
LigaN           .  
DivisionW     -47.1
Liga87N         .

F - Decision Tree

Bevor du einen Decision Tree per Cross-Validation fittest, benötigst du das Kandidatenset für die Tuning Parameter. Erstelle hierzu mit dem Code einen Vektor von möglichen cp Werten.

# Kandidaten für cp
cp_vec <- seq(from = 0, to = 1, length = 100)

Fitte einen Decision Tree, der das Gehalt des Baseballspielers durch alle Features im Datensatz vorhersagt. Beginne mit dem bekannten Code und zusätzlich…

setze das trControl Argument auf das ctrl_cv Objekt.
setze das tuneGrid Argument auf expand.grid(cp = cp_vec).

# Decision Tree 
gehalt_rpart <- train(form = XX ~ .,
                  data = XX,
                  method = "XX",
                  trControl = XX,
                  tuneGrid = XX)

# Decision Tree
gehalt_rpart <- train(form = Gehalt ~ .,
                  data = baseball_train,
                  method = "rpart",
                  trControl = ctrl_cv,
                  tuneGrid = expand.grid(cp = cp_vec))

Plotte das Objekt gehalt_rpart mit plot(). Was verrät dir der Plot? Welcher cp Wert könnte optimal sein?

plot(gehalt_rpart)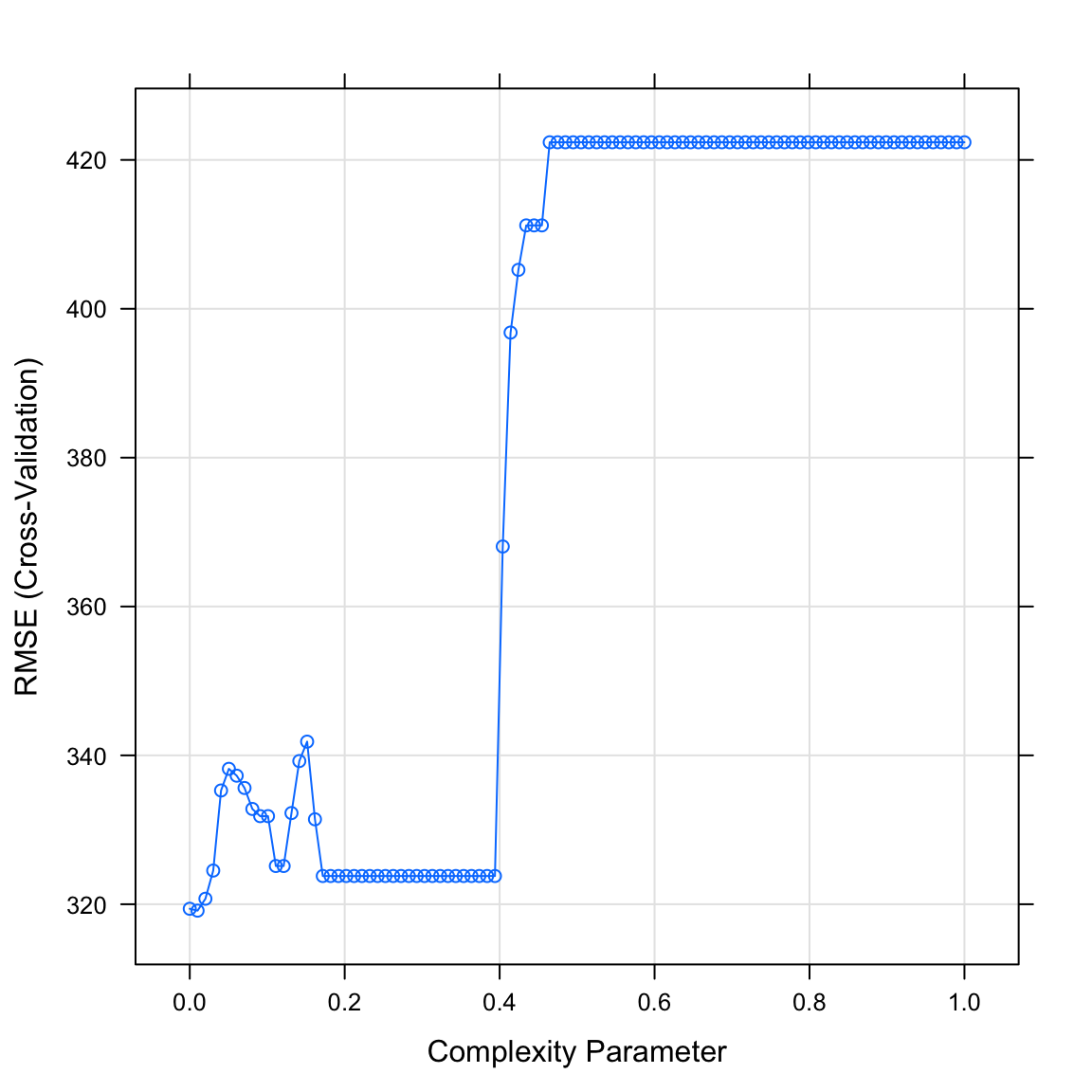

Printe mit dem Code unten den durch die Cross-Validation als besten cp identifizierten Wert. Passt er zum Plot in der letzten Aufgabe?

# Print besten cp Parameter
gehalt_rpart$bestTune$cp

[1] 0.0101

Plotte das finale Modell mit dem folgenden Code.

# Visualisiere den Decision Tree
plot(as.party(gehalt_rpart$finalModel))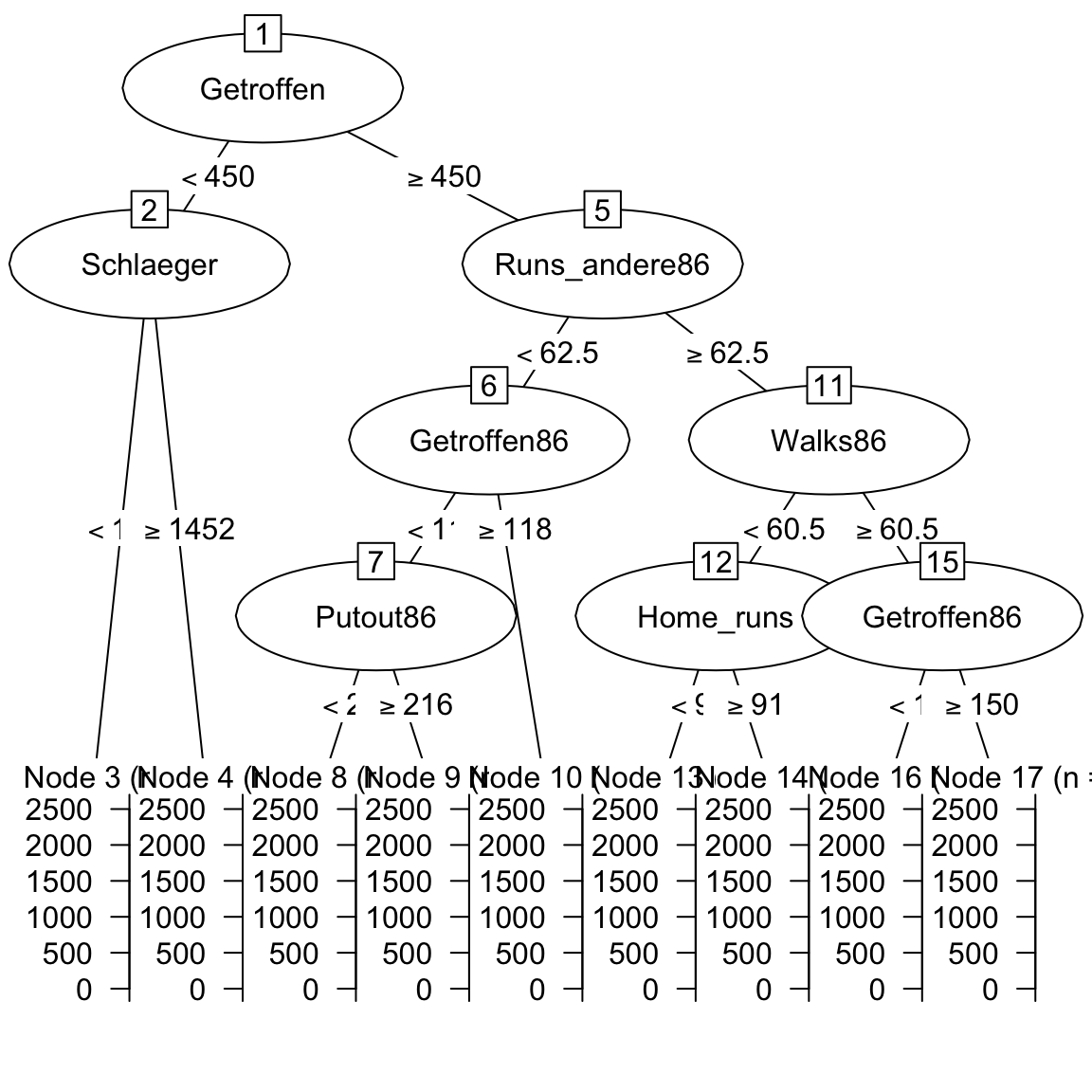

G - Random Forests

Bevor du einen Random Forest per Cross-Validation fittest, benötigst du das Kandidatenset für die Tuning Parameter. Erstelle hierzu mit dem Code einen Vektor von möglichen mtry Werten.

# Kandidaten für mtry
mtry_vec <- 1:10

Fitte einen Random Forest, der das Gehalt des Baseballspielers durch alle Features im Datensatz vorhersagt. Beginne mit dem bekannten Code und zusätzlich…

setze das trControl Argument auf das ctrl_cv Objekt.
setze das tuneGrid Argument auf expand.grid(mtry = mtry_vec).

# Random Forest 
gehalt_rf <- train(form = XX ~ .,
                   data = XX,
                   method = "XX",
                   trControl = XX,
                   tuneGrid = XX)

# Random Forest 
gehalt_rf <- train(form = Gehalt ~ .,
                   data = baseball_train,
                   method = "rf",
                   trControl = ctrl_cv,
                   tuneGrid = expand.grid(mtry = mtry_vec))

Plotte das Objekt gehalt_rf mit plot(). Was verrät dir der Plot? Welche mtry Werte könnten optimal sein?

plot(gehalt_rf)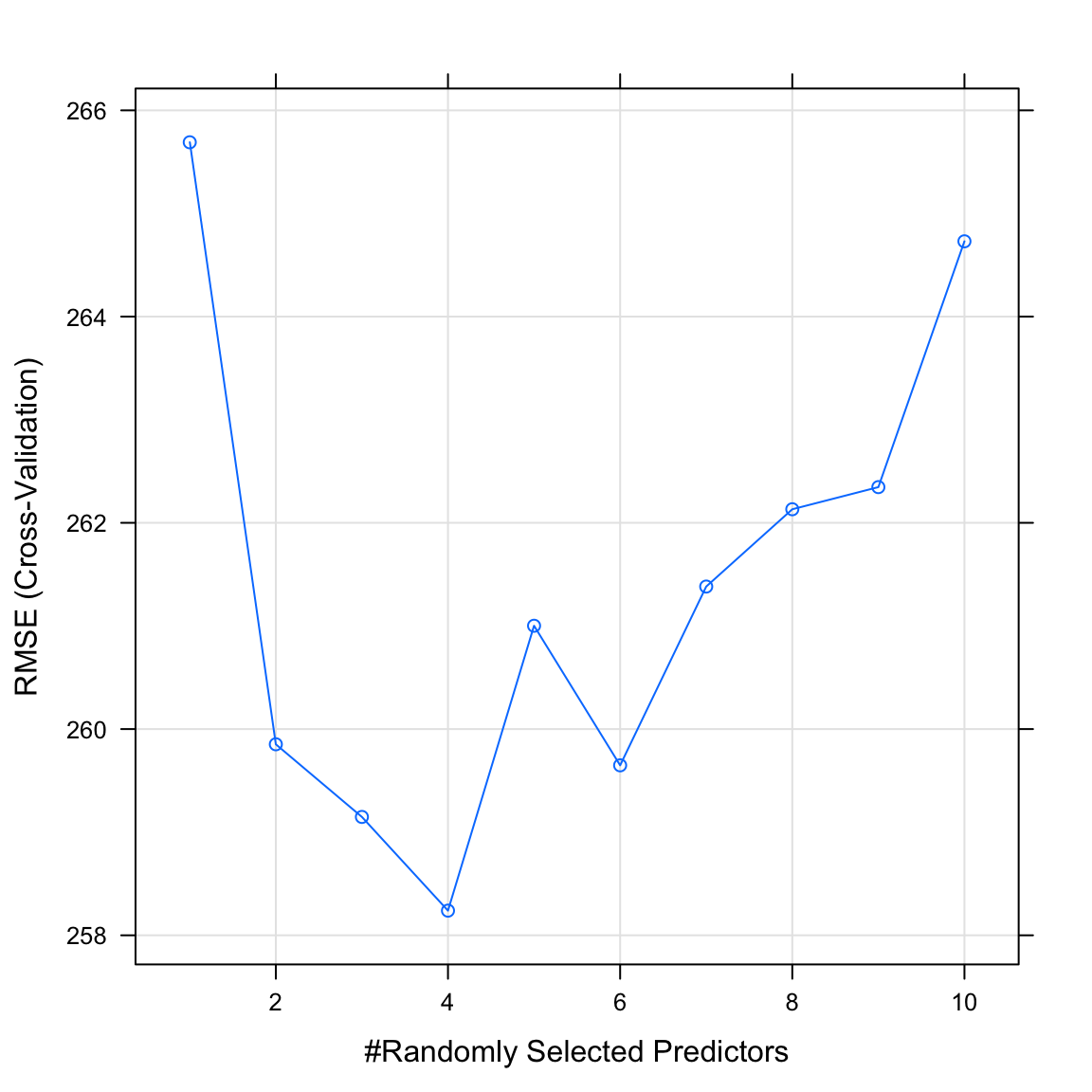

Printe mit dem Code unten den durch die Cross-Validation als bestes mtry identifizierten Wert. Passt er zum Plot in der letzten Aufgabe?

# Printe besten mtry Parameter
gehalt_rf$bestTune$mtry

[1] 4

H - Schätze die Vorhersageperformanz über Cross Validation

Verwende resamples() um die geschätzte Vorhersageleistung der einzelnen Modelle zu bestimmen. Übergebe hierzu die einzelnen gefitteten Modelle (z.b., gehalt_glm) an die Funktion.

# Geschätzte Vorhersageleistung
gehalt_resamples <- resamples(list(glm = XXX,
                                   ridge = XXX, 
                                   lasso = XXX, 
                                   rpart = XXX, 
                                   rf = XXX))

# Geschätzte Vorhersageleistung
gehalt_resamples <- resamples(list(glm = gehalt_glm,
                                   ridge = gehalt_ridge, 
                                   lasso = gehalt_lasso, 
                                   dt = gehalt_rpart, 
                                   rf = gehalt_rf))

Erhalte einen Überblick über die Ergennisse mit summary(gehalt_resamples). Wie interpretierst du den Ouput? Welches Modell hat die beste geschätzte Vorhersageleistung?

I - Berechne tatsächliche Vorhersageleistung

Speichere das Kriterium (Gehalt) der Testdaten baseball_test in einem Objekt namens criterion_test.

# Testkriterium
criterion_test <- XXX$XXX

# Geschätzte Vorhersageleistung
criterion_test <- baseball_test$Gehalt

Verwende predict() um auf bekanntem Wege Vorhersagen für die Testdaten baseball_test auf Basis der Modelle zu bestimmen.

# Vorhersagen der Modelle
ridge_pred <- predict(XXX, newdata = XXX)
lasso_pred <- predict(XXX, newdata = XXX)
rpart_pred <- predict(XXX, newdata = XXX)
rf_pred <- predict(XXX, newdata = XXX)

# Vorhersagen der Modelle
ridge_pred <- predict(gehalt_ridge, newdata = baseball_test)
lasso_pred <- predict(gehalt_lasso, newdata = baseball_test)
rpart_pred <- predict(gehalt_rpart, newdata = baseball_test)
rf_pred <- predict(gehalt_rf, newdata = baseball_test)

Verwende postResample() um die Vorhersagen mit den tatsächlichen Kriteriumswerten zu vergleichen. Welches Modell hat in der Vorhersage der Testdaten die beste Performanz?

postResample(ridge_pred, criterion_test)

    RMSE Rsquared      MAE 
 445.415    0.254  258.965

postResample(lasso_pred, criterion_test)

    RMSE Rsquared      MAE 
 446.113    0.256  262.016

postResample(rpart_pred, criterion_test)

    RMSE Rsquared      MAE 
 496.719    0.248  292.957

postResample(rf_pred, criterion_test)

    RMSE Rsquared      MAE 
 397.953    0.402  214.714

Vergleiche die geschätzten Vorhersageleistungen auf Basis von resamples() (aus der letzten Sektion) mit der Leistung für tatsächliche Vorhersage. Wie gross sind die Unterschiede?

X - Challenges: Abschlussrate

Vergleiche auf Basis der Schritte in diesem Practical die Performanz von Regression, Lasso, Ridge, Decision Tree und Random Forest für die graduation_train und graduation_test Datensätze aus dem letzten Practical. Lass die Modelle das Kriterium Privatuniversität auf Basis aller anderen Features vorhersagen. Nicht vergessen für Klassifikation muss das Kriterium ein factor sein.

Welches Modell ist das beste?
Wie viel besser werden die Modelle durch Model Tuning? Vergleiche mit den Ergebnissen des letzten Practicals.
Setzt Lasso die Gewichte einzelner Features auf 0? Was könnte das für die Relevanz des Features bedeuten?

Y - Challenges: Hauspreise

Vergleiche auf Basis der Schritte in diesem Practical die Performanz von Regression, Lasso, Ridge, Decision Tree und Random Forest für die house_train und house_test Datensätze aus dem letzten Practical. Lass die Modelle das Kriterium Preis auf Basis aller anderen Features vorhersagen.

Welches Modell ist das beste?
Wie viel besser werden die Modelle durch Model Tuning? Vergleiche mit den Ergebnissen des letzten Practicals.
Setzt Lasso die Gewichte einzelner Features auf 0? Was könnte das für die Relevanz des Features bedeuten?

Beispiele

# Schritt 0: Lade Pakete-----------
library(tidyverse)   
library(caret)      
library(partykit)  
library(party)  

# Step 1: Lade und bereite Daten ----------------------

# Training und Testdaten
data_train <- read_csv("1_Data/diamonds_train.csv")
data_test <- read_csv("1_Data/diamonds_test.csv")

# Konvertiere alle character zu factor
data_train <- data_train %>% mutate_if(is.character, factor)
data_test <- data_test %>% mutate_if(is.character, factor)

# Definiere Kriterien
criterion_train <- data_train$price
criterion_test <- data_test$price

# Schritt 2: Definiere die Training-Kontrollparameter -------------

# Verwende 10-fold Cross Validation
ctrl_cv <- trainControl(method = "cv", 
                        number = 10) 

# Scrhitt 3: Trainieree Modelle -----------------------------

# Simple Regression ----
price_glm <- train(form = price ~ carat + depth + table + x + y,
                   data = data_train,
                   method = "glm",
                   trControl = ctrl_cv)


# Zeige Outputs
price_glm
coef(price_glm$finalModel)

# Lasso ----

# Kandidatenset für lambda
lambda_vec <- 10 ^ seq(-3, 3, length = 100)

# Lasso Regression
price_lasso <- train(form = price ~ carat + depth + table + x + y,
                   data = data_train,
                   method = "glmnet",
                   trControl = ctrl_cv,
                   preProcess = c("center", "scale"), # Standardisiere 
                   tuneGrid = expand.grid(alpha = 1,  
                                          lambda = lambda_vec))

# Zeige Outputs
price_lasso 
plot(price_lasso)

# Zeige beste Regularisierungsparameter
price_lasso$bestTune$lambda

# Zeige finales Modell
coef(price_lasso$finalModel, 
     price_lasso$bestTune$lambda)


# Ridge ----

# Kandidatenset für lambda
lambda_vec <- 10 ^ seq(-3, 3, length = 100)

# Ridge Regression
price_ridge <- train(form = price ~ carat + depth + table + x + y,
                     data = data_train,
                     method = "glmnet",
                     trControl = ctrl_cv,
                     preProcess = c("center", "scale"), # Standardisiere
                     tuneGrid = expand.grid(alpha = 0,
                                            lambda = lambda_vec))

# Zeige Outputs
price_ridge
plot(price_ridge)

# Zeige beste Regularisierungsparameter
price_ridge$bestTune$lambda

# Zeige finales Modell
coef(price_ridge$finalModel, 
     price_ridge$bestTune$lambda)


# Decision Trees --------------------------

# Kandidatenset für cp
cp_vec <- seq(0, .1, length = 100)

price_rpart <- train(form = price ~ carat + depth + table + x + y,
                  data = data_train,
                  method = "rpart",
                  trControl = ctrl_cv,
                  tuneGrid = expand.grid(cp = cp_vec))

# Zeige Outputs
price_rpart

# Zeige beste Regularisierungsparameter
plot(price_rpart)
price_rpart$bestTune$cp


# Schritt 3: Vorhersageperformanz in folds ----

# Berechne Performanz
resamples_price <- resamples(list(ridge = price_ridge, 
                                  lasso = price_lasso, 
                                  glm = price_glm))

# Zusammenfassung
summary(resamples_price)


# Schritt 4: Vorhersageevaluation -------------------

# GLM
glm_pred <- predict(price_glm, newdata = data_test)
postResample(pred = glm_pred, obs = criterion_test)

# Ridge
ridge_pred <- predict(price_ridge, newdata = data_test)
postResample(pred = ridge_pred, obs = criterion_test)

# Lasso
lasso_pred <- predict(price_lasso, newdata = data_test)
postResample(pred = lasso_pred, obs = criterion_test)

Datensätze

Datei	Zeilen	Spalten
baseball_train.csv	213	20
baseball_test.csv	50	20
graduation_train.csv	500	18
graduation_test.csv	277	18
house_train.csv	5000	21
house_test.csv	1000	21

`baseball_train` and `baseball_test`

Die baseball_train und baseball_test Datensätze entstammen dem Hitters Datensatz des ISLR Pakets. Sie enthalten Daten über Major League Baseball Spieler aus den Saisons 1986 und 1987.

Name | Beschreibung |

`graduation_train` und `graduation_test`

Die graduation_train und graduation_test Datensätze entstammen dem College Datensatz aus dem ISLR Paket. sie enthalten Statistiken für eine grosse Anzahl US Colleges auf Basis des US News and World Reports aus dem Jahr 1995.

Name	Beschreibung
Privatuniversitaet	Ja oder Nein
Bewerbungen	Anzahl Bewerbungen
Angenommen	Anzahl angenommene Bewerbungen
Eingeschrieben	Anzahl eingeschrieben
Prozent_Top10	Prozent der Studierenden innerhalb Top 10% in High School
Prozent_Top25	Prozent der Studierenden innerhalb Top 25% in High School
Vollzeit	Anzahl Studierende in Vollzeit
Teilzeit	Anzahl Studierende in Teilzeit
Kosten_ausserhalb	Kosten für Studierende aus einem anderen Staat
Kosten_Unterkunft	Kosten für Studierende für Unterkunft und Verpflegung
Kosten_Buecher	Kosten für Studierende für Bücher
Kosten_persoenlich	Kosten für Studierende für Persönliches
Prozent_PhD	Anteil PhDs innerhalb der Dozentenschaft
Prozent_Degree	Anteil Abschlüsse innerhalb der Dozentenschaft
Verhaeltnis_Stud.Doz.	Verhältnis Studierene zu Dozenten
Prozent_Spenden	Anteil Alumnis, die an das College spenden
Kosten_Student	Ausbildungskosten für das College pro Student
Abschlussrate	Abschlussrate

`house_train` and `house_test`

Die house_train und house_test Datensätze enthalten Hauspreise und -Eigenschaften in der King County in den USA, welches die Stadt Seattle beinhaltet. Quelle der Daten ist Kaggle.

Name	Beschreibung
Preis	Preis des Hauses
Schlafzimmer	Anzahl Schlafzimmer
Baeder	Anzahl Bäder
Gesamt_sqft	Gesamtfläche des Hauses in square foot
Grundstück_sqft	Fläche des Grundstücks in square foot
Stockwerke	Anzahl Stockwerke
Uferlage	0 = Nein, 1 = Ja
Besichtigung	Wurde das Haus besichtigt
Zustand	Wie gut ist der Zustand des Hauses
Einstufung	Einstufung gemäss King County Einstufungssystem
Wohnraum_sqft	Wohnraum des Hauses in square foot
Keller_sqft	Kellerraum des Hauses in square foot
Baujahr	Baujahr
Renovationsjahr	Renovationsjahr
Postleitzahl	Postleitzahl
Breitengrad	Breitengrad
Laengengrad	Längengrad
Gesamt_sqft_2015	Gesamtfläche des Hauses in square foot in 2015
Grundstück_sqft_2015	Fläche des Grundstücks in square foot in 2015

Funktionen

Pakete

Paket	Installation
`tidyverse`	`install.packages("tidyverse")`
`caret`	`install.packages("caret")`
`partykit`	`install.packages("partykit")`
`party`	`install.packages("party")`

Funktionen

Funktion	Paket	Beschreibung
`trainControl()`	`caret`	Definiere wie das Modell trainiert wird
`train()`	`caret`	Trainiere (fitte) ein Modell
`predict(object, newdata)`	`stats`	Vorhersage des Kriteriumswerts in `newdata`
`postResample()`	`caret`	Evaluiere Performanz in Regressionsfällen
`confusionMatrix()`	`caret`	Evaluiere Performanz in Klassifikationsfällen

Materialien

Optimizing

Maschinelles Lernen mit R The R Bootcamp

Überblick

Aufgaben

A - Setup

B - Lade die baseball Datensätze

C - Definiere trainControl

C - Regression

D - Ridge Regression

E - Lasso Regression

F - Decision Tree

G - Random Forests

H - Schätze die Vorhersageperformanz über Cross Validation

I - Berechne tatsächliche Vorhersageleistung

X - Challenges: Abschlussrate

Y - Challenges: Hauspreise

Beispiele

Datensätze

baseball_train and baseball_test

graduation_train und graduation_test

house_train and house_test

Funktionen

Pakete

Funktionen

Materialien

Maschinelles Lernen mit R
The R Bootcamp

B - Lade die `baseball` Datensätze

C - Definiere `trainControl`

`baseball_train` and `baseball_test`

`graduation_train` und `graduation_test`

`house_train` and `house_test`