Gemischte Modelle
|
Statistik mit R The R Bootcamp |

|

from rottentomatoes.com
Overview
Am Ende dieses Practicals wirst du wissen, wie du:
- gemischte Modelle in R berechnen kannst.
- p-Werte für feste Effekte extrahieren kannst.
- die richtige Struktur der zufälligen Effekte auswählen kannst.
- gekreuzte und hierarchische zufällige Effekte spezifizieren kannst.
- Varianzkomponenten extrahieren kannst und die Intraklassenkorrelation (ICC) berechnen kannst.
- dein gemischtes Modell visualisieren kannst.
- ein generalisiertes gemischtes Modell berechnen kannst.
Aufgaben
A - Setup
- Öffne dein
TheRBootcampR Project. Darin sollten bereits die Ordner1_Dataund2_Codeenthalten sein. Stelle sicher, dass die Datensätze, welche in derDatensätzeSpalte gelistet sind in deinem1_DataOrdner vorhanden sind.
# Gemacht!- Öffne ein neues R Skript. Am Anfang des Skripts, schreibe deinen Namen und das Datum als Kommentar und speichere das Skript als
GemischteModelle_Practical.Rin deinem2_CodeOrdner.
# Gemacht!- Lade mit
library()dietidyverse,lme4,performance, undparametersPakete.
# Lade benötigte Pakete
library(tidyverse)
library(lme4)
library(performance)
library(parameters)- Unter Verwendung des folgenden Codes, lese die
tomatometer.csvundschools.csvDatensätze ein und speichere sie unter den Namentomundschools.
# Lese tomatometer.csv aus dem 1_Data Ordner
tom <- read_csv(file = "1_Data/tomatometer.csv")
# Lese school.csv aus dem 1_Data Ordner
schools <- read_csv(file = "1_Data/schools.csv")Printe die Datensätze.
Verwende
names(XX),summary(XX), undView(XX)um einen weiteren Überblick über die Daten zu bekommen.Wiederum, führe den Code unten aus um sicherzustellen, dass alle
characterVariablen als Faktoren vorliegen, was den statistischen Modellen hilft kategoriale Variablen richtig zu interpretieren.
# Konvertiere alle character zu factor
tom <- tom %>% mutate_if(is.character, factor)
schools <- schools %>% mutate_if(is.character, factor)B - Rechnen Eines Linearen Gemischten Modells
Im ersten Teil dieses Practicals arbeiten wir mit dem tom Datensatz aus den Folien und testen die Wirkung des zustands einer Person (nuechtern vs. betrunken) auf ihre tomatometer-Bewertung.
- Rechne ein Modell mit nur festen Effekten aus, in welchem du
tomatometersmit demzustandvorhersagst. Speichere das Ergebnis alsFE_modund schaue dir das Ergebnis an.
# Verwende lm, da lmer nur mit mindestens einem zufälligen Effekt funktioniert
FE_mod <- glm(formula = XXX ~ XXX,
data = XXX)
# Inspiziere die Resultate
summary(XXX)# Verwende lm, da lmer nur mit mindestens einem zufälligen Effekt funktioniert
FE_mod <- glm(formula = tomatometer ~ zustand,
data = tom)
# Inspiziere die Resultate
summary(FE_mod)
Call:
glm(formula = tomatometer ~ zustand, data = tom)
Deviance Residuals:
Min 1Q Median 3Q Max
-43.45 -7.64 0.36 7.55 42.55
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 55.446 0.212 261 <2e-16 ***
zustandnuechtern -25.803 0.300 -86 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for gaussian family taken to be 135)
Null deviance: 1807144 on 5994 degrees of freedom
Residual deviance: 809285 on 5993 degrees of freedom
AIC: 46426
Number of Fisher Scoring iterations: 2- Im Moment wird “betrunken” als Referenzkategorie verwendet, sodass der intercept den Mittelwert des Zustands “betrunken” angibt und der slope die Differenz der Mittelwerte der Bewertungen im Zustand “betrunken” und “nuechtern” angibt. Um ein intuitiveres Modell mit “nuechtern” als Referenzkategorie zu erhalten, können wir die Variable
zustanderneut in einen Faktor umwandeln und dabei diesmal die Abfolge der Levels bestimmen. Verwende dafür den untenstehenden Code.
# Wandle die zustand variable in einen Faktor um, mit nuechtern als erstes Level
tom <- tom %>%
mutate(zustand = factor(zustand, levels = c("nuechtern", "betrunken")))- Rechne erneut das Modell der Aufgabe B1.
# Verwende lm, da lmer nur mit mindestens einem zufälligen Effekt funktioniert
FE_mod <- glm(formula = tomatometer ~ zustand,
data = tom)
# Inspiziere die Resultate
summary(FE_mod)
Call:
glm(formula = tomatometer ~ zustand, data = tom)
Deviance Residuals:
Min 1Q Median 3Q Max
-43.45 -7.64 0.36 7.55 42.55
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 29.643 0.212 140 <2e-16 ***
zustandbetrunken 25.803 0.300 86 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for gaussian family taken to be 135)
Null deviance: 1807144 on 5994 degrees of freedom
Residual deviance: 809285 on 5993 degrees of freedom
AIC: 46426
Number of Fisher Scoring iterations: 2Vergleiche die Outputs der Aufgaben B1 und B3. Wie haben sich die Koeffizienten verändert? Weshalb?
Rechne ein gemischtes Modell mit Random Intercepts über die
idder Rater. Zufällige Effekte werden in Klammern in der Modell-formulaspezifiziert. Ein Modell mit nur Random Intercepts trägt allein eine1for dem Gruppierungsfaktor. DasREML = FALSEim untenstehenden Code sagt R, dass das Model mit Maximum Likelihood (ML), statt mit Restricted Maximum Likelihood (REML) gefitted werden soll. Dies ist für die späteren Modellvergleiche wichtig, soll uns aber im Detail nicht weiter beschäftigen.
# Gemischtes Modell mit random intercepts über ids
subj_RI_mod <- lmer(formula = XXX ~ XXX + # Feste Effekte
(1|XXX), # zufällige Effekte
data = XXX, # Daten
REML = FALSE)# Gemischtes Modell mit random intercepts über ids
subj_RI_mod <- lmer(formula = tomatometer ~ zustand + # Feste Effekte
(1|id), # zufällige Effekte
data = tom, # Daten
REML = FALSE)- Unter Verwendung der
summary()Funktion, vergleiche die Outputs des gemischten Modells und des Modells aus B3.
summary(subj_RI_mod)Linear mixed model fit by maximum likelihood ['lmerMod']
Formula: tomatometer ~ zustand + (1 | id)
Data: tom
AIC BIC logLik deviance df.resid
45284 45310 -22638 45276 5991
Scaled residuals:
Min 1Q Median 3Q Max
-3.699 -0.667 0.008 0.673 4.002
Random effects:
Groups Name Variance Std.Dev.
id (Intercept) 31.8 5.64
Residual 103.2 10.16
Number of obs: 5995, groups: id, 200
Fixed effects:
Estimate Std. Error t value
(Intercept) 29.639 0.440 67.4
zustandbetrunken 25.813 0.262 98.4
Correlation of Fixed Effects:
(Intr)
zstndbtrnkn -0.298summary(FE_mod)
Call:
glm(formula = tomatometer ~ zustand, data = tom)
Deviance Residuals:
Min 1Q Median 3Q Max
-43.45 -7.64 0.36 7.55 42.55
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 29.643 0.212 140 <2e-16 ***
zustandbetrunken 25.803 0.300 86 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for gaussian family taken to be 135)
Null deviance: 1807144 on 5994 degrees of freedom
Residual deviance: 809285 on 5993 degrees of freedom
AIC: 46426
Number of Fisher Scoring iterations: 2- Hat sich der Effekt von
zustandverändert? Was hat sich genau am Effekt vonzustandauf die Bewertungen geändert?
# Während sich die Schätzungen der festen Effekte kaum verändert haben, haben
# sich die t-Werte erheblich verändert (der t-Wert für zustandbetrunken in
# FE_mod ist niedriger als der in subj_RI_mod, und der für den Intercept ist um
# 50% gesunken).Interessierst du dich wie die geschätzten Fixed und Random Effects aussehen? Du kannst sie mit
fixef(XX)undranef(XX)aus dem Modellobjekt extrahieren. Probiere es aus.Baue dein gemischtes Modell aus Aufgabe B5 aus, indem du Random Slopes für
zustandüberids hinzufügst. Füge diezustandVariable auf der Linken Seite der Pipe|in dem Teil derformula, in dem die zufälligen Effekte spezifiziert werden.
# Gemischtes Modell mit random intercepts über ids und random slopes für zustand
# über ids
subj_RI_RS_mod <- lmer(formula = XXX ~ XXX + # Feste Effekte
(XXX|XXX), # Zufällige Effekte
data = XXX, # Daten
REML = FALSE)# Gemischtes Modell mit random intercepts über ids und random slopes für zustand
# über ids
subj_RI_RS_mod <- lmer(formula = tomatometer ~ zustand + # Feste Effekte
(zustand|id), # Zufällige Effekte
data = tom, # Daten
REML = FALSE)- Vergleiche die Outputs der drei bisherigen Modelle miteinander. Verwende dazu die
summary()Funktion. Haben sich die Koeffizienten verändert? Was hat sich verändert?
summary(subj_RI_RS_mod)Linear mixed model fit by maximum likelihood ['lmerMod']
Formula: tomatometer ~ zustand + (zustand | id)
Data: tom
AIC BIC logLik deviance df.resid
44912 44952 -22450 44900 5989
Scaled residuals:
Min 1Q Median 3Q Max
-3.569 -0.669 0.022 0.671 3.953
Random effects:
Groups Name Variance Std.Dev. Corr
id (Intercept) 16.6 4.07
zustandbetrunken 37.0 6.08 0.26
Residual 93.6 9.68
Number of obs: 5995, groups: id, 200
Fixed effects:
Estimate Std. Error t value
(Intercept) 29.641 0.338 87.7
zustandbetrunken 25.815 0.498 51.9
Correlation of Fixed Effects:
(Intr)
zstndbtrnkn 0.003 summary(subj_RI_mod)Linear mixed model fit by maximum likelihood ['lmerMod']
Formula: tomatometer ~ zustand + (1 | id)
Data: tom
AIC BIC logLik deviance df.resid
45284 45310 -22638 45276 5991
Scaled residuals:
Min 1Q Median 3Q Max
-3.699 -0.667 0.008 0.673 4.002
Random effects:
Groups Name Variance Std.Dev.
id (Intercept) 31.8 5.64
Residual 103.2 10.16
Number of obs: 5995, groups: id, 200
Fixed effects:
Estimate Std. Error t value
(Intercept) 29.639 0.440 67.4
zustandbetrunken 25.813 0.262 98.4
Correlation of Fixed Effects:
(Intr)
zstndbtrnkn -0.298summary(FE_mod)
Call:
glm(formula = tomatometer ~ zustand, data = tom)
Deviance Residuals:
Min 1Q Median 3Q Max
-43.45 -7.64 0.36 7.55 42.55
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 29.643 0.212 140 <2e-16 ***
zustandbetrunken 25.803 0.300 86 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for gaussian family taken to be 135)
Null deviance: 1807144 on 5994 degrees of freedom
Residual deviance: 809285 on 5993 degrees of freedom
AIC: 46426
Number of Fisher Scoring iterations: 2# Für FE_mod und subj_RI_mod: siehe Antwort zu B7. Die Koeffizienten haben sich
# wiederum nicht verändert, da sich die Gruppenmittelwerte nicht verändert haben.
# Jedoch haben sich die t-Werte wieder stark verändert. Zum Beispiel ist der
# t-Wert des Koeffizienten "zustandbetrunken" in subj_RI_mod 98.31 und derjenige
# im Modell subj_RI_RS_mod "nur" 51.81.- Jeder Film wurde in beiden Zuständen Bewertet. Wir haben also nicht nur Abhängigkeiten in den Daten der Rater, sondern auch der Filme. Um für diese Abhängigkeit zu kontrollieren, können wir unser Modell aus der Aufgabe B10 mit weiteren zufälligen Effekten ausbauen. Füge Random Intercepts über
filmund Random Slopes fürzustandüberfilmzum Modell hinzu. Über das zusätzliche Argumentcontrolwird ein anderer Optimierungsalgorithmus spezifiert, mithilfe dessen das Modell konvergiert. Die details sollen uns für den Moment nicht kümmern; wir freuen uns einfach, dass das Modell konvergiert.
# Gemischtes Modell mit random intercepts über ids und random slopes für zustand
# über ids, sowie random intercepts über film und random slopes für zustand über
# film
max_mod <- lmer(formula = XXX ~ XXX + # Feste Effekte
(XXX|XXX) + (XXX|XXX), # Zufällige Effekte
data = XXX, # Daten
REML = FALSE,
control = lmerControl(optimizer = "bobyqa")) # Optimierungsalgorithmus# Gemischtes Modell mit random intercepts über ids und random slopes für zustand
# über ids, sowie random intercepts über film und random slopes für zustand über
# film
max_mod <- lmer(formula = tomatometer ~ zustand + # Feste Effekte
(zustand|id) + (zustand|film), # Zufällige Effekte
data = tom, # Daten
REML = FALSE,
control = lmerControl(optimizer = "bobyqa")) # Optimierungsalgorithmus- Mit der
check_convergence()Funktion desperformancePaket können wir überprüfen, ob ein Modell konvergiert ist. Wenn die FunktionTRUEzurückgibt, ist alles in Ordnung. Teste, obmax_modkonvergiert ist.
check_convergence(max_mod)[1] TRUE
attr(,"gradient")
[1] 6.24e-07max_modist das maximale, vom Design gerechtfertigten Modell. Was heisst das? Weshalb macht es Sinn, dieses Modell zu spezifizieren?
# Es heisst, dass alle zufälligen Effekte spezifiziert wurden, die gemäss unserer
# Datenstruktur spezifiziert werden können.
# Barr und Kollegen fanden, dass wenn man NICHT das maximale Modell spezifiziert,
# man eine Inflation von Typ-I Fehlern riskiert. Die Resultate der nächsten
# Aufgabe unterstützen diesen Befund. Es gib jedoch auch hier einen Tradeoff,
# doch dazu später mehr.- Vergleiche mit
summary()die Resultate der unterschiedlich Komplexen Modelle, die du bisher gerechnet hast.
summary(max_mod)Linear mixed model fit by maximum likelihood ['lmerMod']
Formula: tomatometer ~ zustand + (zustand | id) + (zustand | film)
Data: tom
Control: lmerControl(optimizer = "bobyqa")
AIC BIC logLik deviance df.resid
41827 41888 -20905 41809 5986
Scaled residuals:
Min 1Q Median 3Q Max
-3.597 -0.668 0.002 0.676 4.284
Random effects:
Groups Name Variance Std.Dev. Corr
id (Intercept) 19.4 4.41
zustandbetrunken 42.9 6.55 0.13
film (Intercept) 24.8 4.98
zustandbetrunken 29.8 5.46 -0.04
Residual 52.6 7.25
Number of obs: 5995, groups: id, 200; film, 15
Fixed effects:
Estimate Std. Error t value
(Intercept) 29.64 1.33 22.3
zustandbetrunken 25.83 1.50 17.3
Correlation of Fixed Effects:
(Intr)
zstndbtrnkn -0.039summary(subj_RI_RS_mod)Linear mixed model fit by maximum likelihood ['lmerMod']
Formula: tomatometer ~ zustand + (zustand | id)
Data: tom
AIC BIC logLik deviance df.resid
44912 44952 -22450 44900 5989
Scaled residuals:
Min 1Q Median 3Q Max
-3.569 -0.669 0.022 0.671 3.953
Random effects:
Groups Name Variance Std.Dev. Corr
id (Intercept) 16.6 4.07
zustandbetrunken 37.0 6.08 0.26
Residual 93.6 9.68
Number of obs: 5995, groups: id, 200
Fixed effects:
Estimate Std. Error t value
(Intercept) 29.641 0.338 87.7
zustandbetrunken 25.815 0.498 51.9
Correlation of Fixed Effects:
(Intr)
zstndbtrnkn 0.003 summary(subj_RI_mod)Linear mixed model fit by maximum likelihood ['lmerMod']
Formula: tomatometer ~ zustand + (1 | id)
Data: tom
AIC BIC logLik deviance df.resid
45284 45310 -22638 45276 5991
Scaled residuals:
Min 1Q Median 3Q Max
-3.699 -0.667 0.008 0.673 4.002
Random effects:
Groups Name Variance Std.Dev.
id (Intercept) 31.8 5.64
Residual 103.2 10.16
Number of obs: 5995, groups: id, 200
Fixed effects:
Estimate Std. Error t value
(Intercept) 29.639 0.440 67.4
zustandbetrunken 25.813 0.262 98.4
Correlation of Fixed Effects:
(Intr)
zstndbtrnkn -0.298summary(FE_mod)
Call:
glm(formula = tomatometer ~ zustand, data = tom)
Deviance Residuals:
Min 1Q Median 3Q Max
-43.45 -7.64 0.36 7.55 42.55
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 29.643 0.212 140 <2e-16 ***
zustandbetrunken 25.803 0.300 86 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for gaussian family taken to be 135)
Null deviance: 1807144 on 5994 degrees of freedom
Residual deviance: 809285 on 5993 degrees of freedom
AIC: 46426
Number of Fisher Scoring iterations: 2- Was hat sich mit der zunehmend komplexen Struktur der zufälligen Effekte verändert?
# Die t-Werte für den Effekt von "zustand" haben sich stark verändert. Jetzt ist
# er "nur" 17.28. Dies ist zwar noch immer substantiell, jedoch zeigt dieser
# Befund auch die Resultate von Barr et al. (2013), die besagen, dass für
# konfirmatorische Hypothesentests immer die maximale Struktur der zufälligen
# Effekte spezifiziert werden sollte, da es sonst zu einer alpha-Fehler-Inflation
# kommen kann (das heisst, dass in diesem Fall die feste Effekte zu häufig als
# statistisch signifikant gewertet werden, selbst wenn dies tatsächlich nicht
# angebracht ist).C - \(R^2\)
Beim rechnen von statistischen Modellen sind wir häufig daran interessiert, einen wie grossen Anteil diese erklären können. In linearen (gemischten) Modellen, wird dies durch das Bestimmtheitsmass \(R^2\) angegeben; for generalisierte (gemischte) Modelle, können wir Pseudo-\(R^2\) Werte berechnen.
- Verwende die
r2()Funktion aus demperformancePaket, um den \(R^2\) Werte des maximalen Modells zu berechnen.
r2(max_mod)# R2 for Mixed Models
Conditional R2: 0.826
Marginal R2: 0.551- Was bedeutet der Output der vorherigen Aufgabe? Was ist das marginal \(R^2\) und was ist das conditional \(R^2\)?
# "marginal r-squared" gibt nur die erklärte Varianz der festen Effekte an.
# In diesem Fall heisst das, dass das maximale Modell mit den festen
# Effekten 55% der in den Daten vorhandenen Varianz erklären kann.
# "conditional r-squared" gibt die erklärte Varianz der festen Effekte UND der
# zufälligen Effekte an. In diesem Fall heisst das, dass das maximale Model
# mit den festen und zufälligen Effekten 83% der in den Daten vorhandenen
# Varianz erklären kann.- Vergleiche die \(R^2\) Werte von
max_modmit denen der weniger komplexen Modelle. Sind die Veränderungen gross? Welche \(R^2\)-Werte haben sich verändert?
r2(max_mod)# R2 for Mixed Models
Conditional R2: 0.826
Marginal R2: 0.551r2(subj_RI_RS_mod)# R2 for Mixed Models
Conditional R2: 0.690
Marginal R2: 0.552r2(subj_RI_mod)# R2 for Mixed Models
Conditional R2: 0.658
Marginal R2: 0.552D - Visualisierung
Häufig ist es hilfreich, unser Modell zu visualisieren. Führe den untenstehenden Code aus, um aus max_mod Koeffizienten zu extrahieren und zu visualieren. Da Plotting kein Schwerpunkt dieses Kurses ist, gehen wir hier aber nicht weiter ins Detail. Falls du Fragen zum Code hast, kannst du uns gerne rufen.
- Visualisiere mit dem untenstehenden Code dein
max_mod.
# Extrahiere feste Effekte
m_line <- fixef(max_mod)
# Extrahiere zufällige Effekte
ranefs <- ranef(max_mod)
predicted <- tibble(
intercept = ranefs$id[,1] + fixef(max_mod)[1],
slope = ranefs$id[,2] + fixef(max_mod)[2])
# Ziehe 15 zufällige Rater um separate Linien für diese zu plotten
rand15 <- sample(1:nrow(predicted), 15)
LMM_plot <- ggplot(tom, aes(zustand, tomatometer)) +
geom_point(colour= "#606061", alpha = .15, size = 2.5)+
geom_segment(aes(x = 1, y = intercept, xend = 2, yend = intercept + slope),
data = predicted %>% slice(rand15), colour = "#EA4B68", size = 1.5,
alpha = .8) +
geom_segment(aes(x = 1, y = m_line[1], xend = 2, yend = sum(m_line)),
colour = "black", size = 2, alpha = 1) +
theme(axis.title.x = element_text(vjust = -1),
axis.title.y = element_text(vjust = 1)) +
theme_bw() +
coord_cartesian(ylim= c(0, 100)) +
theme(
strip.text = element_text(size = 12, face = "bold"),
axis.text = element_text(size = 16),
axis.title = element_text(size = 18,face = "bold")
)
LMM_plot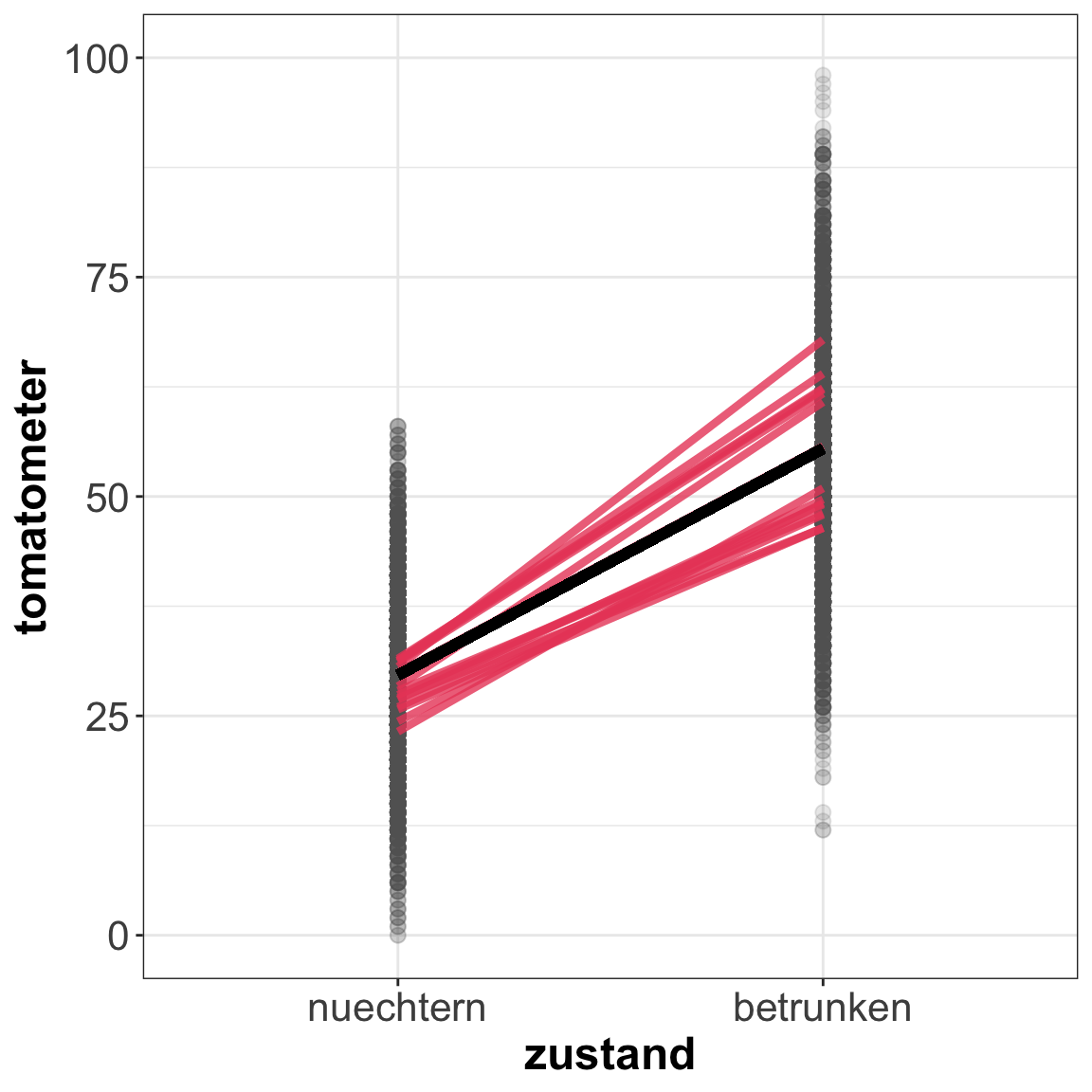
E - p-Werte für Feste Effekte Berechnen
Wie du sicherlich festgestellt hast, enthält der lmer() output keine p-Werte. Das liegt nicht and der Faulheit der Autoren von lme4, sondern daran, dass es noch immer eine Diskussion darum gibt, wie p-Werte für gemischte Modelle am besten berechnet werden sollten. Es gibt jedoch mehrere Möglichkeiten zu testen, ob eine Variable ein signifikanter Prädiktor unserer abhängigen Variable ist. Wir werden uns nun einige davon anschauen.
Likelihood Ratio Test
Eine Möglichkeit p-Werte zu erhalten, besteht darin, einen Likelihood Ratio Test (LRT) durchzuführen. Dafür wird ein Modell einmal mit und einmal ohne den gewünschten festen Effekt gerechnet, wobei alles Andere gleich gehalten wird. Die beiden Modelle werden dann mit dem LRT verglichen (siehe Link oben für Details). Dieser Test funktioniert allerdings nur dann korrekt, wenn die Modelle mit Maximum Likelihood (ML) und nicht mit Restricted Maximum Likelihood (REML) Schätzung gerechnet wurden. Deshalb haben wir immer REML = FALSE verwendet.
- Rechne zuerst ein Modell, in welchem nur die Intercepts (fester Effekt und zufällige Effekte) als Prädiktoren von
tomatometergeschätzt werden.
# Modell mit nur Intercepts als Prädiktoren von Tomatometer
IO_mod <- lmer(formula = XXX ~ 1 + # 1 heisst, dass nur der Intercept geschätzt wird
(1|XXX) + (1|XXX), # Zufällige Effekte
data = XXX, # Daten
REML = FALSE)# Modell mit nur Intercepts als Prädiktoren von Tomatometer
IO_mod <- lmer(formula = tomatometer ~ 1 + # 1 heisst, dass nur der Intercept geschätzt wird
(1|id) + (1|film), # Zufällige Effekte
data = tom, # Daten
REML = FALSE)- Inspiziere den output mit
summary().
summary(IO_mod)Linear mixed model fit by maximum likelihood ['lmerMod']
Formula: tomatometer ~ 1 + (1 | id) + (1 | film)
Data: tom
AIC BIC logLik deviance df.resid
50333 50360 -25163 50325 5991
Scaled residuals:
Min 1Q Median 3Q Max
-2.4127 -0.8192 -0.0296 0.8088 3.1463
Random effects:
Groups Name Variance Std.Dev.
id (Intercept) 27.2 5.21
film (Intercept) 30.4 5.51
Residual 244.2 15.63
Number of obs: 5995, groups: id, 200; film, 15
Fixed effects:
Estimate Std. Error t value
(Intercept) 42.55 1.48 28.7- Rechne nun dasselbe Modell wie gerade eben, aber füge die Variable
zustandals festen Effekt hinzu. Speichere das Modell alsRI_mod. Damit das Modell konvergiert verwenden wir wiederum einen anderen Optimierungsalgorithmus.
# Modell mit zustand als Prädiktor und Random Intercepts für id und film
RI_mod <- lmer(formula = XXX ~ XXX + # Feste Effekte
(1|XXX) + (1|XXX), # Zufällige Effekte
data = XXX, # Daten
REML = FALSE,
control = lmerControl(optimizer = "bobyqa")) # Optimierungsalgorithmus# Modell mit zustand als Prädiktor und Random Intercepts für id und film
RI_mod <- lmer(formula = tomatometer ~ zustand + # Feste Effekte
(1|id) + (1|film), # Zufällige Effekte
data = tom, # Daten
REML = FALSE,
control = lmerControl(optimizer = "bobyqa")) # Optimierungsalgorithmus- Überprüfe mit der
check_convergence()Funktion obRI_modkonvergiert ist.
check_convergence(RI_mod)[1] TRUE
attr(,"gradient")
[1] 8.13e-08- Führe mit der
anova()Funktion einen LRT durch, indem du beide Modellouputs als Argumente spezifizierst. Ist der Unterschied signifikant? What heisst das?
# Rechne einen LRT
anova(XXX, XXX)# Rechne einen LRT
anova(IO_mod, RI_mod)Data: tom
Models:
IO_mod: tomatometer ~ 1 + (1 | id) + (1 | film)
RI_mod: tomatometer ~ zustand + (1 | id) + (1 | film)
npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
IO_mod 4 50333 50360 -25163 50325
RI_mod 5 43220 43254 -21605 43210 7115 1 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# Der Unterschied ist signifikant. Das komplexere Modell ist also signifikant
# besser darin, die Varianz zu erklären. "zustand" ist also ein signifikanter
# PrädiktorKonfidenzintervall
Diese Methode berechnet keinen p-Wert, sondern die Konfidenzintervalle um die Parameter. Dann testen wir, ob 0 in den Konfidenzintervallen enthalten ist. Falls nicht, betrachten wir die jeweiligen Zusammenhänge als signifikant.
- Zur Berechnung von Konfidenzintervallen verwenden wir die
confint()Funktion deslme4Pakets. Berechne damit die Konfidenzintervalle vonRI_modund speichere den Output alsci_mod. Achtung: Das Berechnen der Konfidenzintervalle dauert eine Weile.
# Berechne Konfidenzintervalle für die festen Effekte
ci_mod <- confint(XXX)# Berechne Konfidenzintervalle für die festen Effekte
ci_mod <- confint(RI_mod)Computing profile confidence intervals ...- Printe das
ci_modObjekt. Unterstützen die Konfidenzintervalle die Konklusion die du aus dem LRT und den t-Werten gezogen hast?
ci_mod 2.5 % 97.5 %
.sig01 5.19 6.41
.sig02 4.03 8.37
.sigma 8.29 8.60
(Intercept) 26.52 32.75
zustandbetrunken 25.40 26.25Weitere Tests
- Weitere Möglichkeiten p-Werte zu erhalten sind das Anschauen der t-Werte (t > 2 kann als Signifikanz interpretiert werden) oder einen Wald test mit der
p_value()Funktion desparametersPakets. Berechne mitp_value()die p-Werte vonRI_mod.
# Berechne p-Werte für die festen Effekte
p_value(XXX)# Berechne p-Werte für die festen Effekte
p_value(RI_mod) Parameter p
1 (Intercept) 1.17e-86
2 zustandbetrunken 0.00e+00- Statt einem Wald test wird auch die Kenward-Roger Approximation empfohlen. Um die p-Werte mit dieser Methode zu berechnen, können wir in der
p_value()Funktionmethod = "kenward"setzen. Da dies aber sehr lange dauern kann, musst du diese Aufgabe nicht ausführen.
# Berechne p-Werte für die festen Effekte
p_value(RI_mod, method = "kenward")F - Signifikanz von Zufälligen Effekten (Modellselektion)
Vielleicht erinnerst du dich and das keep it maximal Prinzip, welches besagt, dass wir immer das maximale Modell spezifizieren sollen (Barr, Levy, Scheepers, & Tily, 2013). Nun ist es aber so, dass das maximale Model einen Powerverlust bedeuten kann. Daher kann es sinnvoll sein, eine Datengetriebene Auswahl der Struktur der zufälligen Effekte durchzuführen (Matuschek, Kliegl, Vasishth, Baayen, & Bates, 2017). Um es mit den Worten von Matuschek und Kollegen auszudrücken (frei übersetzt): “[Ein] sparsames gemischtes Modell […], welches nur Varianzkomponenten beinhaltet, die von den Daten gestützt werden, verbessert die Balance zwischen Typ I Fehler und Power” (p. 305). Um diese Balance zu finden, werden wir LRTs durchführen.
Bei diesen LRTs sollten wir nicht das normale 5% \(\alpha\)-Niveau verwenden. Eine Begründung finden wir wiederum in Matuschek und Kollegen (2017; p. 308; wiederum frei übersetzt):
Im Kontext der Modellauswahl ist es wichtig dem Reflex zu widerstehen, \(\alpha_{LRT} = 0.05\) zu wählen. \(\alpha_{LRT}\) kann nicht wie üblich als den “erwarteten Modellselektions Typ I Fehlerrate” interpretiert werden, sondern als relatives Gewicht von Modellkomplexität und Goodness-Of-Fit. Zum Beispiel, die Wahl von \(\alpha_{LRT} = 0\) impliziert eine unendlich starke Bestrafung für Modellkomplexität und daher würde immer das minimale Modell gewählt, ungeachtet der von den Daten gelieferten Evidenz. Die Wahl von \(\alpha_{LRT} = 1\) impliziert eine unendlich starke Bestrafung für Goodness-Of-Fit und das maximale Modell würde daher immer gewählt. Ein \(\alpha_{LRT} = 0.05\) könnte daher eine unverhälnissmässig starke Bestrafung der Modellkomplexität bedeuten und dadurch ein reduziertes [also weniger komplexes] Modell wählen, selbst wenn die Daten ein komplexeres Modell favorisieren würden.
Wir folgen in dieser Übung dem Vorschlag von Matuschek und Kollegen und verwenden \(\alpha_{LRT} = 0.2\). Da die anova() Funktion \(\alpha = 0.05\) verwendet, müssen wir diesen Test selber implementieren.
- Zunächst müssen wir das Modell anpassen, dessen Komplexität im Vergleich zum maximalen Modell eine Stufe niedriger ist. Überlegen dir, welches Modell das wäre, und notiere dir die Antwort als Kommentar in deinem Skript. Nicht schummeln, indem du die nächste Aufgabe ansiehst!
# Dies ist nur ein Platzhalter, um den Platz bis zur nächsten Aufgabe zu vergrößern, um es für dich leichter zu machen, nicht zu schummeln.
# Hier gibt es nichts zu sehen...
# Nur eine kleine Nebenbemerkung (was eigentlich sehr interessant ist, so dass du
# vielleicht weiterlesen möchtest, auch wenn dies dem Zweck dieses Teils
# widerspricht, dich daran zu hindern dir zuerst die Antworten ansehen; also
# erwäge, zuerst die Aufgabe zu erledigen und erst dann diese schrecklich
# interessante Nebenbemerkung zu lesen):
# Wusstest du, dass der Grund, warum R den Pfeil "<-" als Zuordnungsoperator
# verwendet ist, weil R auf der Programmiersprache S basiert, welche wiederum
# auf APL basiert?
# Nun wurde APL offenbar auf einer bestimmten Tastatur entworfen, die eine
# "<-" Taste hatte. Zudem gab es kein "==" um die Gleichheit von Objekten zu
# testen. Also Gleichheit wurde mit "=" getestet und "<-" wurde als
# Zuweisungsoperator gewählt (Informationen aus diesem Blogpost:
# https://colinfay.me/r-assignment/).- Die Antwort auf die letzte Frage ist, dass du die Korrelation zwischen den zufälligen Effekten, also zwischen den Random Intercepts und den Random Slopes, auf Null setzst. Verwende dazu den doppelten Balken “
||” in der Syntax, in der die zufälligen Effekte spezifiziert werden, also(Datenmatrix||Gruppierungsvariable). Fitte dieses Modell.
# Eingeschränktes gemischtes Modell, mit random Intercepts über, und Random Slopes
# für zustand über id und film
con_mod <- lmer(formula = XXX ~ XXX + # Feste Effekte
(XXX||XXX) + (XXX||XXX), # Zufällige Effekte
data = XXX, # Daten
REML = FALSE,
control = lmerControl(optimizer = "bobyqa")) # Optimierungsalgorithmus# Eingeschränktes gemischtes Modell, mit random Intercepts über, und Random Slopes
# für zustand über id und film
con_mod <- lmer(formula = tomatometer ~ zustand + # Feste Effekte
(zustand||id) + (zustand||film), # Zufällige Effekte
data = tom, # Daten
REML = FALSE,
control = lmerControl(optimizer = "bobyqa")) # OptimierungsalgorithmusWarning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
unable to evaluate scaled gradientWarning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
Model failed to converge: degenerate Hessian with 1 negative eigenvalues- Überprüfe mit
check_convergence()ob das Modell konvergiert ist.
check_convergence(con_mod)[1] TRUE
attr(,"gradient")
[1] 0.000476Dieses Modell ist nicht konvergiert. Das kann passieren und es ist nicht immer einfach herauszufinden, weshalb ein Modell nicht konvergiert. Eine weiterführende Möglichkeit ist, Bayesianische Methoden mit MCMC sampling zu verwenden (zum Beispiel mit dem
rstanarmPaket), und zu schauen ob dieses Modell konvergiert. Wir beschränken uns hier aber auf frequentistische Analysen und werden hier daher nicht weiter forschen. In der Praxis kann es aber durchaus Sinn machen, weiter zu untersuchen, ob man das Modell mit einer anderen Methode zum konvergieren bringt. Um die Übung fortsetzen zu können, tun wir für den Moment so, als ob das Modell konvergiert wäre.Jetzt ist es an der Zeit, den LRT vorzubereiten. Der Unterschied in der deviance (definiert als -2 * die LogLikelihood) zweier Modelle ist approximativ \(\chi^2\)-verteilt. Dadurch können wir die Signifikanz eines Unterschiedes testen, indem wir überprüfen, ob der erhaltene \(\chi^2\) Wert grösser als ein bestimmter kritischer Wert ist. Wir verwenden unser \(\alpha_{LRT}\) um den kritischen Wert zu erfahren. Führe dazu folgenden Code aus.
alpha <- .2 # bestimme das alpha-Niveau
kW <- qchisq(1 - alpha, df = 2) # bestimme den kritischen Wert, ab dem ein Unterschied
# als signifikant zu betrachten ist. Wir haben zwei
# Freiheitsgrade, da das eingeschränkte Modell zwei
# Freiheitsgrade mehr als das maximale Modell hat
# (da zwei Parameter, die Kovarianzen, weniger geschätzt werden)- Nun können wir den Unterschied der deviances der Modelle berechnen, indem wir die deviance des maximalen Modells von derjenigen des eingeschränkten Modells subtrahieren. Extrahiere die deviances der beiden Modelle mihilfe der
deviance()Funktion und speichere das Resultat alsd_diff.
d_diff <- deviance(XXX) - deviance(XXX)d_diff <- deviance(con_mod) - deviance(max_mod)- Teste, ob der Unterschied in der deviance gross genug ist, um gemäss dem von uns gewählten \(\alpha_{LRT}\) als signifikant zu gelten. Tipp: Teste ob
d_diffgrösser ist, als der kritische WertkW.
# Teste, ob der Unterschied gross genug ist, um als signifikant zu gelten
d_diff > kW[1] FALSE- Das Resultat der vorherigen Aufgabe war
FALSE. Was heisst das? Würdest du jetzt mit dem maximalen Modell weiterarbeiten? Was würde es bedeuten, wenn das ResultatTRUEgewesen wäre; wie würden dann deine nächsten Schritte aussehen?
# FALSE als Resultat bedeutet in diesem Fall, dass der Unterschied in der deviance
# der beiden Modelle nicht gross genug war, als dass wir das maximale Modell als
# signifikant besser einschätzen würden. Wir würden also nicht das maximale Modell
# verwenden. Wäre das Resultat TRUE, würde das bedeuten, dass das maximale Modell
# signifikant besser fitted und daher verwendet werden sollte.X - Herausforderungen
Mehr zu p-Werten für feste Effekte: Parametrisches Bootstrapping
Ein weiterer Signifikanztest für feste Effekte ist das parametrische Bootstrapping. Dieses ist insbesondere dann sinnvoll anzuwenden, wenn sich der p-Wert am Rande des Alpha-Niveaus befindet. Beim parametrischen Bootstrapping werden aus den bestehenden Daten wiederholt Stichproben mit Zurücklegen gezogen (resampling mit Zurücklegen) und das Modell an jeder dieser Stichproben gerechnet. Damit erhalten wir eine empirische Verteilung des interessierenden Parameters oder Effekts. Der Nachteil dieser Methode ist, dass sie ziemlich lange dauern kann.
- Für lineare gemischte Modelle (angewendet mit
lmer()) kannst du diePBmodcomp()Funktion despbkrtestPakets nutzen. Schaue dir die Hilfe-Funktion vonPBmodcomp()so an:
?PBmodcomp- Benutze nun die
PBmodcomp()Funktion um p-Werte für das Modell zu erhalten. Du wirst dazu ein weniger komplexes Modell spezifizieren müssen, gegen welches getestet werden soll. Benutze dazuIO_mod. Da dieses Vorgehen ziemlich lange dauern kann, benutze hier nur 50 Simulationen (setze diese Zahl höher, wenn du tatsächliche Analysen durchführst).
# Führe parametrisches Bootstrapping durch
pb_mod <- PBmodcomp(largeModel = XXX,
smallModel = XXX,
nsim = XXX)# Führe parametrisches Bootstrapping durch
pb_mod <- PBmodcomp(largeModel = max_mod,
smallModel = IO_mod,
nsim = 50)- Lasse dir das
pb_modObjekt anzeigen und schaue dir die Resultate an. Unterscheiden sich die Resultate von denen der anderen Tests die du zuvor angewendet hast? Ist der mit parametrischem Bootstrappen ermittelte p-Wert vergleichbar mit demjenigen des Likelihood Ratio Tests?
pb_modBootstrap test; time: 33.95 sec;samples: 50; extremes: 0;
large : tomatometer ~ zustand + (zustand | id) + (zustand | film)
small : tomatometer ~ 1 + (1 | id) + (1 | film)
stat df p.value
LRT 8516 5 <2e-16 ***
PBtest 8516 0.02 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Intra-Klassen Korrelation (ICC)
Die intra-Klassen Korrelation (ICC) ist “der Anteil der durch die in der Population vorhandenen Gruppenstruktur erklärten Varianz” (Hox, 2002, S. 15). Es wird berechnet, indem die Zwischengruppenvarianz durch die Summe der Innergruppen- und der Zwischengruppenvarianz (d.h., die totale Varianz) geteilt wird.
- Berechne die ICC des Maximalmodells mit der
icc()Funktion aus demperformancePaket.
icc(max_mod)# Intraclass Correlation Coefficient
Adjusted ICC: 0.612
Conditional ICC: 0.275- Oft wird ein ICC basierend auf dem reinen Intercepts-Modell mit Random Intercepts berechnet. In Aufgabe C1 hast du dieses Modell bereits gerechnet und unter
IO_modabgespeichert. Berechne nun die ICC für dieses Modell.
icc(IO_mod)# Intraclass Correlation Coefficient
Adjusted ICC: 0.191
Conditional ICC: 0.191- Jetzt mache dasselbe für das Modell
RI_mod, welches vom ModellIO_mod, welches du gerade benutzt hast, nur dadurch abweicht, dass es feste Effekte enthält.
icc(RI_mod)# Intraclass Correlation Coefficient
Adjusted ICC: 0.473
Conditional ICC: 0.212- Vergleiche die Ergebnisse der beiden letzten Aufgaben. Hat sich etwas verändert? Überlege dir, was diese Änderungen zu bedeuten haben.
Gekreuzte versus geschachtelte zufällige Effekte
Bisher haben wir uns ausschliesslich mit gekreuzten zufälligen Effekten beschäftigt. Nun werden wir uns auch Daten mit geschachtelten zufälligen Effekten anschauen, wo jedes Level eines geschachtelten Faktors nur innerhalb eines einzigen Levels eines übergeordneten Faktors auftritt. Ein beliebtes Beispiel dafür ist der Fall von Klassen innerhalb von Schulen. Jede Klasse ist nur Teil einer einzigen Schule, deshalb sind hier die Klassen geschachtelt innerhalb der Schulen.
Um herauszufinden, ob zufällige Effekte gekreuzt oder geschachtelt sind, musst du normalerweise etwas über das Studiendesign wissen, da die Struktur oft nicht einfach aus den Faktor-Levels ersichtlich ist. In unserem Beispiel der Klassen geschachtelt in Schulen wäre ein potentiell problemantischer Fall beispielsweise die Bezeichnung der Klassen durch Nummerierung innerhalb der Schulen statt über alle Schulen hinweg. Zum Beispiel enthielte Schule 1 Klassen 1 bis 10 und Schule 2 Klassen 1 bis 6. Natürlich ist dann Klasse 1 der Schule 1 nicht dieselbe wie Klasse 1 der Schule 2. Was jedoch für dich offensichtich erscheinen mag, ist nicht offensichtlich für R. R weiss nichts über die Konzepte von Schulen und Klassen, deshalb muss du ihm sagen, ob die Faktoren geschachtelt sind oder nicht, indem du die entsprechende Syntax in der Formel verwendest. Jetzt stelle dir den Fall vor, wo Klassen in Schulen geschachtelt sind, nun aber über alle Schulen hinweg nummeriert sind, also von 1 bis zur totalen Anzahl an Klassen im Datensatz. Somit hat jede Klasse eine eindeutige Bezeichnung. Ist dies der Fall, spielt es keine Rolle wie du die Struktur spezifizierst.
- Für diese Aufgaben arbeitest du mit dem
schoolDatensatz, welchen du bereits in Abschnitt A geladen hast. Erstelle unter Verwendung dertable()Funktion eine Kreuztabelle von Schulen und Klassen.
table(XXX, XXX)table(schools$school, schools$class)
a b c d
I 50 50 50 50
II 50 50 50 50
III 50 50 50 50
IV 50 50 50 50
V 50 50 50 50
VI 50 50 50 50- Rechne ein gemischtes Modell mit Random Intercepts für Klassen geschachtelt in Schulen, in welchem Extraversion (
extra) mit Offenheit (open) und der sozialen Bewertung (social) vorhergesagt wird. Speichere das Modell alshier_mod. Tipp: Die geschachtelte Struktur der zufälligen Effekte wird mit folgender Syntax spezifiziert:(1|higher_level_variable/lower_level_variable).
# Hierarchisches gemischtes Modell
hier_mod <- lmer(formula = extra ~ open + social + # Dies sind die festen Effekte
(1|school/class), # Dies sind die geschachtelten zufälligen Effekte
data = schools, # Hier werden die Daten spezifiziert
REML = FALSE)- Ist das Modell konvergiert? Überprüfe dies mit
check_convergence().
check_convergence(hier_mod)[1] TRUE
attr(,"gradient")
[1] 1.51e-05- Schaue dir die Ergebnisse des Modells mit
summary()an.
summary(hier_mod)Linear mixed model fit by maximum likelihood ['lmerMod']
Formula: extra ~ open + social + (1 | school/class)
Data: schools
AIC BIC logLik deviance df.resid
3545 3575 -1766 3533 1194
Scaled residuals:
Min 1Q Median 3Q Max
-10.015 -0.334 0.015 0.341 10.580
Random effects:
Groups Name Variance Std.Dev.
class:school (Intercept) 8.186 2.861
school (Intercept) 77.864 8.824
Residual 0.967 0.984
Number of obs: 1200, groups: class:school, 24; school, 6
Fixed effects:
Estimate Std. Error t value
(Intercept) 6.00e+01 3.66e+00 16.39
open 6.03e-03 4.96e-03 1.22
social 5.18e-04 1.85e-03 0.28
Correlation of Fixed Effects:
(Intr) open
open -0.054
social -0.050 -0.006- Rechne nun dasselbe Modell nochmals, jedoch diesmal mit gekreuzten random intercepts, wie in den vorherigen Abschnitten, anstelle der geschachtelten random intercepts. Speichere das Modell als
cross_mod.
# Hierarchisches gemischtes Modell
cross_mod <- lmer(formula = extra ~ open + agree + # Dies sind die festen Effekte
(1|school) + (1|class), # Dies sind die gekreuzten zufälligen Effekte
data = schools, # Hier werden die Daten spezifiziert
REML = FALSE)- Überprüfe, ob das Modell konvergiert ist.
check_convergence(cross_mod)[1] TRUE
attr(,"gradient")
[1] 6.91e-06- Schaue dir die Ergebnisse mit der
summary()Funktion an.
summary(cross_mod)Linear mixed model fit by maximum likelihood ['lmerMod']
Formula: extra ~ open + agree + (1 | school) + (1 | class)
Data: schools
AIC BIC logLik deviance df.resid
4716 4746 -2352 4704 1194
Scaled residuals:
Min 1Q Median 3Q Max
-7.898 -0.544 0.012 0.531 8.237
Random effects:
Groups Name Variance Std.Dev.
school (Intercept) 81.17 9.01
class (Intercept) 5.61 2.37
Residual 2.78 1.67
Number of obs: 1200, groups: school, 6; class, 4
Fixed effects:
Estimate Std. Error t value
(Intercept) 60.02428 3.89319 15.42
open 0.01084 0.00834 1.30
agree -0.00545 0.00959 -0.57
Correlation of Fixed Effects:
(Intr) open
open -0.085
agree -0.086 -0.008- Haben sich die Resultate im Vergleich zu denjenigen mit geschachtelten zufälligen Effekten verändert?
# Es gibt Unterschiede in den t-Werten und den Schätzwerten für die festen Effekte.
# Ausserdem haben sich die geschätzten Varianzen der zufälligen Effekte verändert,
# sowie die Anpassungsgüte des Modells, und zwar ist das Modell mit den gekreuzten
# zufälligen Effekten schlechter angepasst.Mehr zur Auswahl zufälliger Effekte
- In Aufgabe D6 hast du herausgefunden, dass das eingeschränkte Modell, in welchem die Korrelationen zwischen den zufälligen Effekten auf Null gesetzt werden, nicht signifikant schlechter war als das maximale Modell. Wenn du also eine konfirmatorische Hypothese testen würdest, solltest du dieses Modell anstelle des maximalen Modells annehmen. Wir haben in dieser Aufgabe die Rückwärtselimination aber nicht weitergeführt. Dies wollen wir hier nachholen. Rechne nun ein Modell mit Random Intercepts und Slopes über die Rater, jedoch ohne Korrelationen dazwischen, und mit Random Intercepts über die Filme.
# Eingeschränktes Modell mit Random Intercepts und Slopes über die Rater, ohne
# Korrelationen dazwischen, und mit Random Intercepts über die Filme
con_mod2 <- lmer(formula = tomatometer ~ zustand + # Dies sind die festen Effekte
(zustand||id) + (1|film), # Dies sind die zufälligen Effekte
data = tom, # Hier werden die Daten spezifiziert
REML = FALSE,
control = lmerControl(optimizer = "bobyqa")) # verwende einen anderen
# Optimizer um Konvergenz-
# Probleme zu verhindern- Führe nun das Vorgehen aus Abschnitt D durch um herauszufinden welches der beiden Modelle beibehalten werden sollte. Hinweis: Das Argument
dfin derqchisq()Funktion wird hier aufdf = 1gesetzt, da diese beiden Modelle sich um nur einen Freiheitsgrad unterscheiden.
# Alpha ist immer noch dasselbe
alpha <- .2 # Spezifiziere das Alpha-Niveau
kW1 <- qchisq(1 - alpha, df = 1) # Ermittle den kritischen Wert über welchem die
# Differenz signifikant ist. Diesmal haben wir
# nur einen Freiheitsgrad, da das komplexere
# Modell nur einen Parameter mehr hat als das
# einfachere Modell
# Ermittle die Differenz in der Deviance zwischen den beiden Modellen
d_diff <- deviance(con_mod2) - deviance(con_mod)
# Teste, ob diese Differenz grösser als der zuvor ermittelte kritische Wert und
# damit signifikant ist
d_diff > kW1[1] TRUE- Zu welcher Schlussfolgerung bist du gelangt? Welches Modell sollten wir beibehalten?
# Das Modell con_mod, in dem die Korrelationen auf Null gesetzt sind würde beibehalten
# werden, da das maximale Modell nicht signifikant besser war, und die einfacheren
# Modelle signifikant schlechter abschnitten. Da dieses Modell allerdings nicht
# konvergierte, das maximale Modell jedoch schon, könnte es in diesem Fall trotzdem
# Sinn machen das maximale Modell auszuwählen.Generalisierte lineare gemischte Modelle
- Nun werden wir uns generalisierte lineare gemischte Modelle anschauen. Lade dazu den Datensatz
cancer_remission.csvund speichere ihn untercr.
cr <- read_csv(file = "1_Data/cancer_remission.csv")Parsed with column specification:
cols(
remission = col_double(),
CancerStage = col_character(),
LengthofStay = col_double(),
Experience = col_double(),
DID = col_double()
)- Schaue dir die Daten an. Es handelt sich um einen Teil von simulierten Daten von UCLA Institute for Digital Research and Education Search.
cr
summary(cr)
View(cr)- Sage die Krebsremissionsrate (
remission) durch das Krebsstadium (CancerStage), die Dauer des Patientenaufenthalts (LengthofStay), die Erfahrung des Arztes (Experience), und durch random intercepts über die Ärzte (DID) vorher. Benutze dazu dieglmerFunktion mitfamily = binomial. Benutze auch hier, wie schon in früheren Aufgaben, den “bobyqa” Optimizer.
cr_mod <- glmer(formula = XXX ~ XXX + XXX + XXX +
(1 | XXX),
data = XXX,
family = binomial, # Damit sagst du glmer, dass es eine logistische Regression rechnen soll
control = glmerControl(optimizer = "bobyqa"))cr_mod <- glmer(formula = remission ~ CancerStage + LengthofStay + Experience +
(1 | DID),
data = cr,
family = binomial, # Damit sagst du glmer, dass es eine logistische Regression rechnen soll
control = glmerControl(optimizer = "bobyqa"))- Ist das Modell konvergiert?
check_convergence(cr_mod)[1] TRUE
attr(,"gradient")
[1] 2.43e-06- Schaue dir die Ergebnisse an.
summary(cr_mod)Generalized linear mixed model fit by maximum likelihood (Laplace
Approximation) [glmerMod]
Family: binomial ( logit )
Formula: remission ~ CancerStage + LengthofStay + Experience + (1 | DID)
Data: cr
Control: glmerControl(optimizer = "bobyqa")
AIC BIC logLik deviance df.resid
7436 7485 -3711 7422 8518
Scaled residuals:
Min 1Q Median 3Q Max
-3.589 -0.447 -0.203 0.406 6.963
Random effects:
Groups Name Variance Std.Dev.
DID (Intercept) 3.87 1.97
Number of obs: 8525, groups: DID, 407
Fixed effects:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.3738 0.5094 -4.66 3.2e-06 ***
CancerStageII -0.4126 0.0737 -5.60 2.2e-08 ***
CancerStageIII -0.9991 0.0958 -10.43 < 2e-16 ***
CancerStageIV -2.3143 0.1550 -14.93 < 2e-16 ***
LengthofStay -0.1207 0.0328 -3.68 0.00023 ***
Experience 0.1196 0.0265 4.50 6.7e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr) CncSII CnSIII CncSIV LngthS
CancerStgII 0.015
CancrStgIII 0.059 0.493
CancerStgIV 0.070 0.334 0.318
LengthofSty -0.303 -0.265 -0.337 -0.290
Experience -0.923 -0.004 -0.008 -0.013 -0.011- Extrahiere den \(R^2\) Wert für dieses Modell mit der
r2().
r2(cr_mod)# R2 for Mixed Models
Conditional R2: 0.585
Marginal R2: 0.097Hinweis: Generalisierte lineare gemischte Modelle zu rechnen und zu interpretieren kann ziemlich anspruchsvoll sein und uns fehlt hier die Zeit, diese detaillierter zu behandeln. Falls du mehr darüber wissen möchtest, kannst du dir dieses Tutorial oder die Referenzen unter Ressourcen genauer anschauen.
Beispiele
# Lade Pakete
library(lme4)
library(parameters)
library(pbkrtest)
library(performance)
# schaue die sleepstudy daten aus dem lme4 Paket
head(sleepstudy)
# Hilfeseite des sleepstudy Datensatzes
?sleepstudy
# Modell mit nur festen Effekten, zur Vorhersage von Reaktionszeiten mit der Anzahl
# Tage an Schlafentzug als Prädiktor
sleep_FE <- glm(formula = Reaction ~ Days, data = sleepstudy)
# Modelloutput
summary(sleep_FE)
# gemischtes Modell mit nur Random Intercepts über Teilnehmende
sleep_IO <- lmer(formula = Reaction ~ 1 + (1|Subject),
data = sleepstudy,
REML = FALSE)
# Modelloutput
summary(sleep_IO)
# gemischtes Modell mit Schlafentzug als Prädiktor und Random Intercepts über
# Teilnehmende
sleep_RI <- lmer(formula = Reaction ~ Days + (1|Subject),
data = sleepstudy,
REML = FALSE)
# Modelloutput
summary(sleep_RI)
# überprüfe ob das Modell konvergiert ist
check_convergence(sleep_RI)
# berechne p-Werte für die festen Effekte mit Kenward-Roger Approximation
p_value(sleep_RI, method = "kenward")
# alternativ, berechne p-Werte mit der anova() Funktion
anova(sleep_IO, sleep_RI)
# gemischtes Modell mit Random Intercepts und Random Slopes für Schlafentzug über
# Teilnehmende, ohne die Kovarianz zwischen Random Intercepts und Random Slopes zu
# schätzen
sleep_nc <- lmer(formula = Reaction ~ Days + (Days||Subject),
data = sleepstudy,
REML = FALSE)
# überprüfe ob das Modell konvergiert ist
check_convergence(sleep_nc)
# Modelloutput
summary(sleep_nc)
# maximales Modell
sleep_max <- lmer(formula = Reaction ~ Days + (Days|Subject),
data = sleepstudy,
REML = FALSE)
# überprüfe ob das Modell konvergiert ist
check_convergence(sleep_max)
# Modelloutput
summary(sleep_max)
### Auswahl der zufälligen Effekte
# setze alpha auf .2
alpha <- .2
# berechne kritischen Wert ab welchem die Differenz signifikant ist
kW <- qchisq(1 - alpha, df = 1)
# berechne die Differenz zwischen den deviances
d_diff <- deviance(sleep_nc) - deviance(sleep_max)
# teste ob die Differenz grösser als der kritische Wert ist
d_diff > kW
# die Kovarianz bringt keinen grossen Zusatznutzen. Wie sieht es mit den
# Random Slopes aus?
d_diff <- deviance(sleep_RI) - deviance(sleep_nc)
# teste ob die Differenz grösser als der kritische Wert ist
d_diff > kW # -> behalte Random Intercepts und verwende sleep_nc
# berechne Bestimmteitsmass
r2(sleep_nc)
# berechne Intraklassenkorrelation
icc(sleep_nc, adjusted = TRUE)
### Visualisierung
# extrahiere feste Effekte
m_line <- fixef(sleep_nc)
# extrahiere zufällige Effekte
ranefs <- ranef(sleep_nc)
predicted <- tibble(
intercept = ranefs$Subject[,1] + fixef(sleep_nc)[1],
slope = ranefs$Subject[,2] + fixef(sleep_nc)[2])
# ziehe 10 Teilnehmende um ihre Trajektorien zu plotten
rand10 <- sample(1:nrow(predicted), 10)
LMM_plot <- ggplot(sleepstudy, aes(Days, Reaction)) +
geom_point(colour= "#606061", alpha = .15, size = 2.5)+
geom_segment(aes(x = 0, y = intercept, xend = 9, yend = intercept + slope * 9),
data = predicted %>% slice(rand10), colour = "#EA4B68", size = 1.5,
alpha = .8) +
geom_segment(aes(x = 0, y = m_line[1], xend = 9, yend = m_line[1] + 9 * m_line[2]),
colour = "black", size = 2, alpha = 1) +
theme(axis.title.x = element_text(vjust = -1),
axis.title.y = element_text(vjust = 1)) +
theme_bw() +
theme(
strip.text = element_text(size = 12, face = "bold"),
axis.text = element_text(size = 16),
axis.title = element_text(size = 18,face = "bold")
)
LMM_plotDatasets
| File | Rows | Columns |
|---|---|---|
| tomatometer.csv | 5995 | 4 |
| schools.csv | 1200 | 7 |
| cancer_remission.csv | 8525 | 5 |
Der tomatometer.csv Datensatz enthält Tomatometerbewertungen von 200 Ratern, die je 15 Filme, einmal im nüchternen und einmal im betrunkenen Zustand bewertet haben.
Der schools.csv Datensatz enthält Selbsteinschätzungen von 1200 Schülern aus unterschiedlichen Klassen von 6 Schulen, auf den Facetten Extraversion, Offenheit für Neues, Verträglichkeit und einem social score.
Der cancer_remission.csv Datensatz enthält Daten zur Remission von Lungenkrebs von Patienten.
tomatometer.csv
| Variable | Beschreibung |
|---|---|
| id | Rater id |
| film | Film id von M1 bis M15 |
| zustand | Der Zustand, in welchem die Bewertungen durchgeführt wurden ("nuechtern", oder "betrunken") |
| tomatometer | Tomatometerbewertung von von 0 bis 100 |
schools.csv
| Variable | Beschreibung |
|---|---|
| id | Schüler id (geschachtelt unter class) |
| extra | Extraversion von 0 bis 100 |
| open | Offenheit von 0 bis 100 |
| agree | Verträglichkeit von 0 bis 100 |
| social | Social |
| class | Schulklasse (geschachtelt unter school; levels "a", "b", "c" und "d") |
| school | Schule (levels "I", "II", "III", "IV") |
cancer_remission.csv
| Variable | Beschreibung |
|---|---|
| remission | Ist der Krebs in Remission (0 = Nein, 1 = Ja) |
| CancerStage | Vier unterschiedliche Krebsstadien (levels "I", "II", "III", "IV") |
| LengthofStay | Dauer des Spitalaufenthaltes (Wert von 1 bis 10) |
| Experience | Erfahrung des Arztes (Wert von 7 to 29, wahrscheinlich in Jahren) |
| DID | Arzt id |
Funktionen
Pakete
| Paket | Installation |
|---|---|
tidyverse |
install.packages("tidyverse") |
lme4 |
install.packages("lme4") |
performance |
install.packages("performance") |
parameters |
install.packages("parameters") |
pbkrtest |
install.packages("pbkrtest") |
Funktionen
| Funktion | Paket | Beschreibung |
|---|---|---|
lmer |
lme4 |
Rechne ein lineares gemischtes Modell |
glmer |
lme4 |
Rechne ein generalisiertes gemischtes Modell |
fixef |
lme4 |
Extrahiere Koeffizienten der festen Effekte |
ranef |
lme4 |
Extrahiere Koeffizienten der zufälligen Effekte |
anova |
stats |
Funktion um einen likelihood ratio test zu rechnen |
confint |
stats |
Berechne Konfidenzintervalle |
deviance |
stats |
Extrahiere deviances |
qchisq |
stats |
“Quantile” Funktion der \(\chi^2\) Verteilung um kritische \(\chi^2\) Werte zu berechnen |
PBmodcomp |
pbkrtest |
Parametrischer Bootstrap zur Berechnung von p-Werten |
check_convergence |
performance |
Teste, ob ein Modell konvergiert ist. |
p_value |
parameters |
Berechne p-Werte für feste Effekte von gemischten Modellen mit unterschiedlichen Methoden |
r2 |
performance |
Berechne Bestimmtheitsmass \(R^2\) |
icc |
performance |
Berechne Intraklassenkorrelation |
Quellen
Texte (Englisch)
Eine gute, nicht-technische Einführung in gemischte Modelle: Buchkapitel An introduction to linear mixed modeling in experimental psychology von Henrik Singmann und David Kellen.
Eine technischere Einführung bieted das Kapitel zu gemischten Modellen in Analysis of Longitudinal and Cluster-Correlated Data von Nan Laird.
Ein frei erhältliches Tutorial über gemischte Modelle gibt es hier.
Eine Einführung in das Bestimmtheitsmass und die Intraklassenkorrelation im Zusammenhang mit gemischten Modellen bietet der Artikel The coefficient of determination R2 and intra-class correlation coefficient from generalized linear mixed-effects models revisited and expanded von Shinichi Nakagawa, Paul Johnson, und Holger Schielzeth.
Eine eher technische Einführung in gemischte Modelle mit lme4 bietet der Artikel Fitting Linear Mixed-Effects Models Using lme4 von Douglas Bates, Martin Mächler, Benjamin Bolker, und Steven Walker.
Ein Klassiker zur Regressionsanalyse, inklusive gemischten Modelle: das Buch Data Analysis Using Regression and Multilevel/Hierarchical Models von Andrew Gelman und Jennifer Hill.
Ein weiteres, hervorragendes Buch über Regressionsanalyse bietet das Buch Statistical Rethinking von Richard McElreath.