A - Setup

1. Öffne dein TheRBootcamp R project. Es sollte die Ordner 1_Data und 2_Code enthalten. Stelle sicher, dass du alle Datensätze, welche im Datensätze Tab aufgelistet sind, in deinem 1_Data Ordner hast.

2. Öffne ein neues R Skript. Schreibe deinen Namen, das Datum und “Lineare Modelle II Practical” als Kommentare an den Anfang des Skripts.

## NAME
## DATUM
## Lineare Modelle II Practical

3. Speichere das neue Skript unter dem Namen lineare_modelle_II_practical.R im 2_Code Ordner.

4. Lade das Paket tidyverse.

library(tidyverse)

5. Verwende die read_csv() Funktion um wein.csv einzulesen.

# Lese Daten ein
wein <- read_csv(file = "1_Data/wein.csv")

6. Printe den Datensatz.

7. Verwende names(XX), summary(XX), und View(XX) um einen weiteren Überblick über die Daten zu bekommen.

8. Wiederum, führe den Code unten aus um sicherzustellen, dass alle character Variablen als Faktoren vorliegen, was den statistischen Modellen hilft kategoriale Variablen richtig zu interpretieren.

# Konvertiere alle character zu factor
wein <- wein %>% mutate_if(is.character, factor)

B - Gruppenvergleiche: t.test versus Regression

1. In diesem Abschnitt geht es darum den Effekt der Farbe (Prädiktor) des Weins, rot oder weiss, auf die Qualität des Weines zu prüfen. Verwende hierzu zunächst den Code unten um zwei Vektoren zu erstellen, die jeweils die Qualitätswerte für weisse und rote Weine beinhalten.

# Qualitätsvektoren nach Farbe
weiss <- wein %>% filter(Farbe == 'weiss') %>% pull(Qualität)
rot <- wein %>% filter(Farbe == 'rot') %>% pull(Qualität)

2. Verwende nun das t.test() template unten um die beiden Vektoren mit einem t-Test miteinander zu vergleichen. Du brauchst das Ergebnis nicht zu speichern.

# t-test
t.test(x = XX, y = XX)

# t-test
t.test(x = weiss, y = rot)

    Welch Two Sample t-test

data:  weiss and rot
t = 10, df = 2951, p-value <2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 0.195 0.289
sample estimates:
mean of x mean of y 
     5.88      5.64 

3. Was verrät dir der Output des t-Tests über den Unterschied weisser und roter Weine in der wahrgenommenen Qualität? Die Antwort findest du in der zweiten Zeile (beginnend mit t=..) zusammen mit der letzten Zeile.

4. Ja, weisse Weine wurden 0.241886 (Differenz der beiden Mittelwerte) Punkte als Qualitativ wertiger wahrgenommen und dieser Unterschied ist signifikant. Versuche nun das selbe Ergebnis mit einer Regression zu erzielen.

# Regression
wein_lm <- lm(formula = XX ~ XX, 
              data = XX)

# Regression
wein_lm <- lm(formula = Qualität ~ Farbe, 
              data = wein)

5. Printe zunächst einmal das Objekt und betrachte die Regressionsgewichte. Kommen dir eine oder sogar beide der Zahlen bekannt vor?

6. Genau, das Regressionsgewicht für Farbe spiegelt exakt den Unterschied der beiden Mittelwerte wieder. Was repräsentiert dann der Intercept? Den Wert derjenigen Kategorie, der R den Wert 0 zugewiesen hat. Dies ist bei ursprünglich character Variablen i.d.R. diejenige Kategorie die alphabetisch früher kommt, d.h., 'rot' < 'weiss'.

7. Lasse dir jetzt die summary() für das Modell ausgeben und vergleiche Freiheitsgrade, t- und p-Wert mit denen aus dem t-Test.

# summary
summary(wein_lm)

Call:
lm(formula = Qualität ~ Farbe, data = wein)

Residuals:
   Min     1Q Median     3Q    Max 
-2.878 -0.878  0.122  0.364  3.122 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   5.6360     0.0217  259.92   <2e-16 ***
Farbeweiss    0.2419     0.0250    9.69   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.867 on 6495 degrees of freedom
Multiple R-squared:  0.0142,    Adjusted R-squared:  0.0141 
F-statistic: 93.8 on 1 and 6495 DF,  p-value: <2e-16

8. Die Werte im t-Test stimmen trotz der gleichen Schätzwerte für die Gewichte nicht ganz überein. Dies liegt daran, dass die t.test() Funktion per Default eine Variante rechnet die erlaubt, dass die Varianzen in den beiden Gruppen (rot und weiss) unterschiedlich sind, die Regression dagegen, geht stets davon aus, dass diese gleich sind, was wir im Detail in der Session zu robuste Statistiken besprechen werden. Rechne den t-Test noch einmal, diesmal mit dem zusätzlichen Argument var.equal = TRUE.

# t-test
t.test(x = XX, y = XX, var.equal = )

# t-test
t.test(x = weiss, y = rot, var.equal = TRUE)

    Two Sample t-test

data:  weiss and rot
t = 10, df = 6495, p-value <2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 0.193 0.291
sample estimates:
mean of x mean of y 
     5.88      5.64 

9. Ordnung ist eingekehrt. Alle Werte im t-test und der Regression sollten jetzt identisch sein, was daran liegt, dass die beiden Modelle nun exakt identisch sind.

C - Gruppenvergleiche: Kodierung

1. Per Default verwendet R die sogenannte Dummy-Kodierung, in der eine Ausprägung den Wert 0 erhält und eine andere den Wert 1. Eine alternative Kodierung existiert in der Effektkodierung, die stattdessen die Werte -1 und 1 vergibt. Um die Konsequenzen dieser beiden Kodierungen direkt zu vergleichen, erstelle zunächst für jede Kodierung eine neue Variable im Datensatz unter Verwendung des Codes unten.

# Kodierungen der Farbe
wein <- wein %>% mutate(Farbe_dummy = ifelse(Farbe == 'rot', 0, 1),
                        Farbe_effekt = ifelse(Farbe == 'rot', -1, 1))

2. Rechne nun zwei Regressionen, jeweils eine mit einer der beiden Farbkodierungen als Prädiktor und speichere sie ab als wein_dummy und wein_effekt.

# Regression dummy
wein_dummy <- lm(formula = XX ~ XX, 
                 data = XX)

# Regression effekt
wein_effekt <- lm(formula = XX ~ XX, 
                  data = XX)

# Regression dummy
wein_dummy <- lm(formula = Qualität ~ Farbe_dummy, 
                 data = wein)

# Regression effekt
wein_effekt <- lm(formula = Qualität ~ Farbe_effekt, 
                  data = wein)

3. Printe nun die beiden Objekte und vergleiche die Gewichte. Diejenigen der Dummy-Kodierung sollten dir bekannt vorkommen. Wie verhalten sich die Gewichte der Effektkodierung dagegen? Erkennst du den Zusammenhang?

4. Der Effekt der Farbe unter der Effektkodierung entspricht genau der Hälfte des Effekts unter der Dummykodierung und um dies auszugleichen hat sich der Intercept auch um genau den selben Wert verändert, nur in die andere Richtung. Verifiziere die Gewichte mit den einfachen Rechnungen im Code unten.

# Dummy-Kodierung
mean(rot) # intercept

[1] 5.64

mean(weiss) - mean(rot) # gewicht farbe

[1] 0.242

# EffekKodierung
(mean(rot) + mean(weiss))/2 # intercept

[1] 5.76

mean(weiss) - (mean(rot) + mean(weiss))/2 # gewicht farbe

[1] 0.121

5. Vergleiche nun die summary() der beiden Modelle. Was unterscheidet sich, und was nicht?

# Regression dummy
summary(wein_dummy)

Call:
lm(formula = Qualität ~ Farbe_dummy, data = wein)

Residuals:
   Min     1Q Median     3Q    Max 
-2.878 -0.878  0.122  0.364  3.122 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   5.6360     0.0217  259.92   <2e-16 ***
Farbe_dummy   0.2419     0.0250    9.69   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.867 on 6495 degrees of freedom
Multiple R-squared:  0.0142,    Adjusted R-squared:  0.0141 
F-statistic: 93.8 on 1 and 6495 DF,  p-value: <2e-16

# Regression effekt
summary(wein_effekt)

Call:
lm(formula = Qualität ~ Farbe_effekt, data = wein)

Residuals:
   Min     1Q Median     3Q    Max 
-2.878 -0.878  0.122  0.364  3.122 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)    5.7570     0.0125  461.04   <2e-16 ***
Farbe_effekt   0.1209     0.0125    9.69   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.867 on 6495 degrees of freedom
Multiple R-squared:  0.0142,    Adjusted R-squared:  0.0141 
F-statistic: 93.8 on 1 and 6495 DF,  p-value: <2e-16

6. Die Kodierung hat ausgenommen die Skalierung des Regressionsgewichts und des zugehörigen Standardfehlers für Farbe keinen Einfluss. t-Wert und Signifikanz sind identisch. Einzig der Intercept ändert sich wesentlich, da er unter der Effektkodierung tatsächlich weiter von Null entfernt ist.

C - Interaktionen

1. Der erste Abschnitt hat gezeigt, dass weisser Wein gegenüber Rotem bevorzugt wurde. Könnte dies daran liegen, dass nicht für andere Variablen kontrolliert wurde? Oder könnte es sein, dass dieser Unterschied nur unter bestimmten Bedingungen gilt, d.h., dass es Moderatoren für den Effekt der Farbe gibt? Rechne eine Regression die zusätzlich Alkohol mit aufnimmt und verknüpfe die Prädiktoren mit * sodass auch die Interaktion berücksichtigt wird.

# Regression mit Interaktion
wein_lm <- lm(formula = XX ~ XX * XX, 
              data = XX)

# Regression mit Interaktion
wein_lm <- lm(formula = Qualität ~ Farbe * Alkohol, 
              data = wein)

2. Printe das Objekt und betrachte die Gewichte. Wie interpretierst du die einzelnen Werte?

3. Folgendermassen lassen sich die Gewichte interpretieren: Unter Berücksichtigung von Alkohol und der Interaktion, werden weisse Weine um .7 besser bewertet. Unter Berücksichtigung der Farbe (d.h. für Farbe == ‘rot’) und der Interaktion, führt ein Anstieg von einem Volumenprozent zu einer Verbesserung der wahrgenommenen Qualität von .36. Unter Berücksichtigung von Farbe und Alkohol, führt die Interaktion, also das Produkt der beiden Prädiktoren zu einer Veränderung von -.05. Dies ist so zu interpretieren, dass der Effekt von Alkohol unter Weissweinen um genau diese Grösse kleiner ist. Dies bedeutet im Umkehrschluss dass der Effekt von Farbe unter hoch-alkoholischen Weinen kleiner ausfällt. Verwendet den Code unten um diese Ergebnisse zu visualisieren. Gelb bedeutet Weisswein, lila Rotwein.

# Visualisierung
ggplot(data = wein, 
       aes(x = Alkohol, y = Qualität, col = Farbe, alpha = .01)) + 
  scale_color_manual(values = viridis::cividis(2)) + 
  geom_jitter(width=2,height=1.5,size=.1) + theme_minimal() + theme(legend.position = 'none') +
  geom_smooth(data = wein %>% filter(Farbe == 'weiss'), method = 'lm') + 
  geom_smooth(data = wein %>% filter(Farbe == 'rot'), method = 'lm')

`geom_smooth()` using formula 'y ~ x'
`geom_smooth()` using formula 'y ~ x'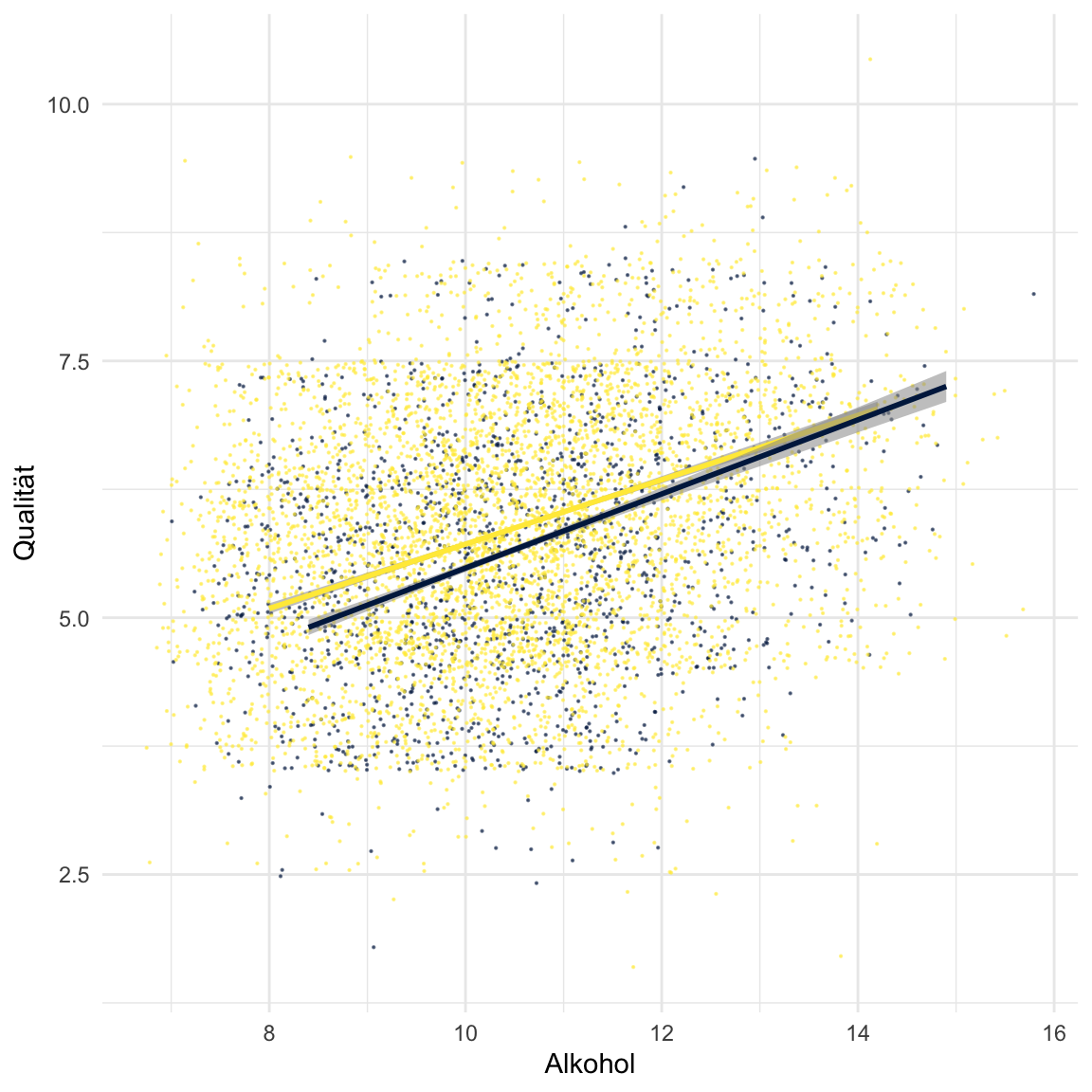

4. Lasse dir nun die summary() anzeigen und inspiziere die t-Werte und Signifikanzen. Welche Prädiktoren sind signifikant?

5. Alle drei Prädiktoren sind signifikant. t-Wert und Signifikanz sind am extremsten für Alkohol, jedoch ist das Gewicht für Alkohol nur halb so gross. Wie ist dies zu erklären?

6. Genau die Gewichte hängen auch von der Skalierung der Prädiktoren ab. Rechne nun die Regression noch einmal, aber diesmal mit skalierten Prädiktoren. Siehe Code unten.

# Skalierungsfunktion
skaliere = function(x) (x - mean(x))/sd(x)

# Regression mit skalierten Prädiktoren
wein_lm <- lm(formula = XX ~ XX * XX, 
              data = XX %>% mutate_if(is.numeric, skaliere))

# Skalierungsfunktion
skaliere = function(x) (x - mean(x))/sd(x)

# Regression mit skalierten Prädiktoren
wein_lm <- lm(formula = Qualität ~ Farbe * Alkohol, 
              data = wein %>% mutate_if(is.numeric, skaliere))

7. Printe zunächst einmal das Objekt und betrachte die Gewichte. Alle Werte haben sich substantiell verändert. Insbesondere hat nun Alkohol das zweifach höhere Gewicht. Wie sind diese neuen Gewichte zu interpretieren, wenn du bedenkst, dass nach der Skalierung alle Variablen eine Standardabweichung = 1 haben?

8. Nach Skalierung sind die Gewichte als Veränderungen in Standardabweichungen zu interpretieren. Z.B., eine Veränderung von einer Standardabweichungen in Alkohol führt demnach zu einer Veränderung von .4928 Standardabweichungen in der Qualität. Am meisten hat sich der Intercept verändert. Wie interpretiert ihr diesen unter der Skalierung?

9. Der Intercept ist der geschätzte Mittelwert des Kriteriums für den Fall in dem alle Prädiktoren Null sind. Ohne Skalierung ist dieser Fall schwer zu interpretieren, da Null nicht vorkommen muss in den Prädiktoren. Unter der Skalierung ändert sich dies aber, denn nun haben alle Prädiktoren, mit Ausnahme des Faktors Farbe einen Mittelwert von Null. Das heisst der Intercept spiegelt die Qualität für ein mittleres Level von Alkohol, rote Weine und keine Interaktion in Standardabweichungen wieder. Dies kannst du wiederum in der Visualisierung nachvollziehen. Benutze den Code unten und suche den Punkt auf der lila Linie für Alkohol = 0.

# Visualisierung
ggplot(data = wein %>% mutate_if(is.numeric, skaliere), 
       aes(x = Alkohol, y = Qualität, col = Farbe, alpha = .01)) + 
  scale_color_manual(values = viridis::cividis(2))  +
  geom_jitter(width=2,height=1.5,size=.1) + theme_minimal() + theme(legend.position = 'none') +
  geom_smooth(data = wein %>% mutate_if(is.numeric, skaliere) %>% filter(Farbe == 'weiss'), method = 'lm') + 
  geom_smooth(data = wein %>% mutate_if(is.numeric, skaliere) %>% filter(Farbe == 'rot'), method = 'lm')

`geom_smooth()` using formula 'y ~ x'
`geom_smooth()` using formula 'y ~ x'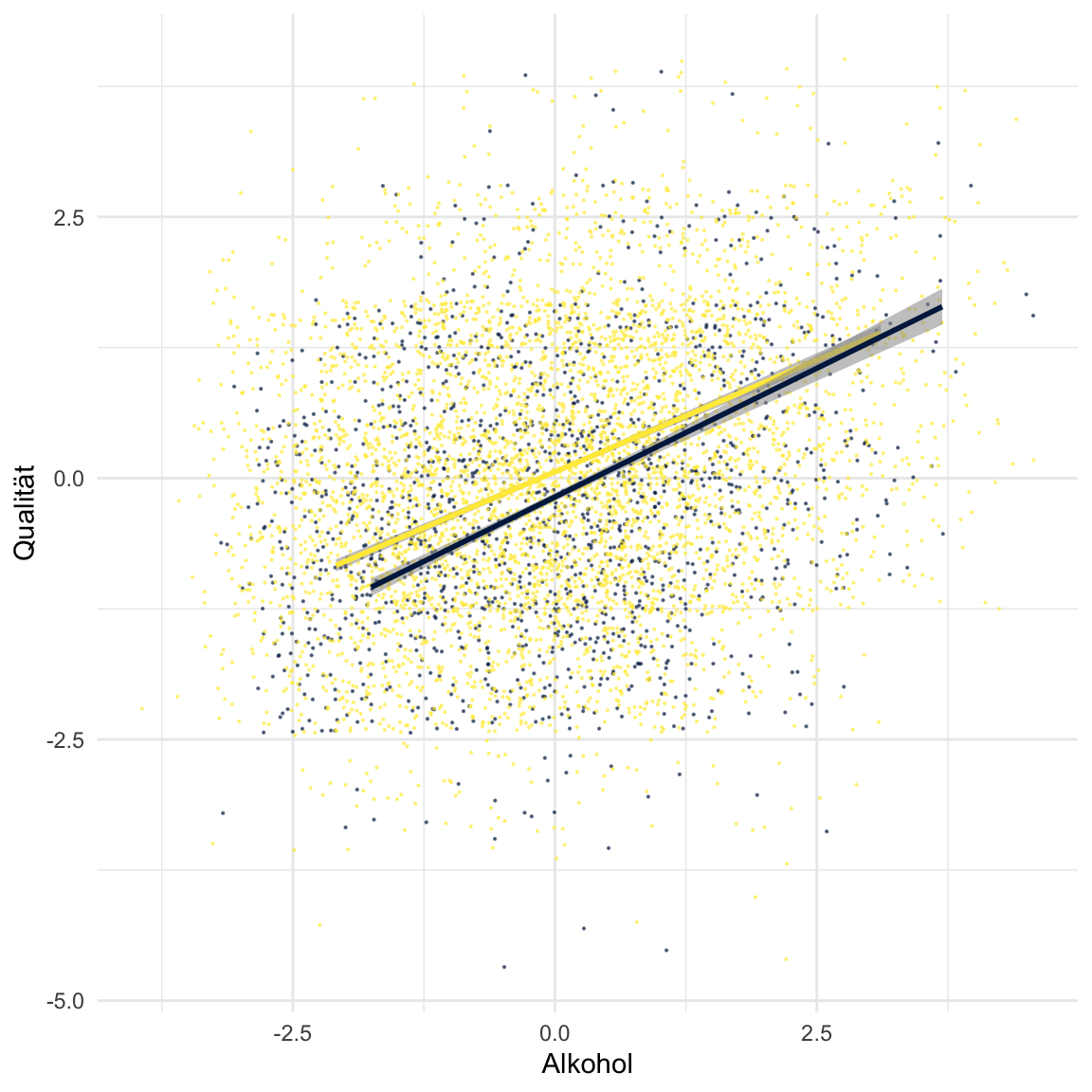

10. Schaue dir nun die summary() an. Was hat sich verändert bzgl. t-Werten, Signifikanzen, und Standardfehlern, und R-squared?

11. Ein grosser und in diesem Fall der Einzige Einfluss besteht auf die Variable Farbe, welche als einzige nicht mit standardisiert wurde. Vor der Standardisierung von Alkohol war Farbe beinahe perfekt mit der Interaktion korreliert, was zu einem extrem aufgeblasenen Standardfehler geführt hat. Die Standardisierung hat diese Korrelation jedoch stark reduziert, so dass der Standardfehler auf das Niveau der anderen Prädiktoren gefallen ist. In der Konklusion lohnt es sich beinahe immer die die Prädiktoren (oder auch das Kriterium) zu standardisieren, wenn ein Vergleich der Gewichte und Signifikanzen von Interesse ist.

wein.csv

Der wein.csv Datensatz enthält aus den Jahren 2004 bis 2007 des Comissão De Viticultura Da Região Dos Vinhos Verdes, der Offiziellen Zertifizierungsagentur des Vinho Verde in Portugal.

Name	Beschreibung
Qualität	Qualitätsurteil über den Wein von 1-9
Farbe	Roter oder weisser Wein
Gelöste_Säure	Konzentration der im Wein gelösten Säuren
Freie_Säure	Konzentration der verflüchtigbaren Säuren
Citronensäure	Citronensäurekonzentration im Wein
Restzucker	Zuckerkonzentration im Wein
Chloride	Chloridkonzentration im Wein
Freie_Schwefeldioxide	Konzentration der verflüchtigbaren Schwefeldioxide
Gesamt_Schwefeldioxide	Konzentration der Schwefeldioxide insgesamt
Dichte	Dichte des Weins
pH_Wert	pH-Wert des Weins. Je kleiner, desto saurer.
Sulphate	Sulphatkontration im Wein
Alkohol	Alkoholkonzentration im Wein in %

Pakete

Package	Installation
tidyverse	install.packages("tidyverse")

Funktionen

Function	Package	Description
lm	stats	Fitte ein lineares Modell
fitted	stats	Extrahiere vorhergesagte Werte
residuals	stats	Extrahiere Residuen

Books

• Discovering Statistics with R von Andy Field ist sehr gut
• YaRrr! The Pirate’s Guide to R hat hilfreiche und unterhaltsame Kapitel zu Statistik mit R.